yourSql 2

--2022.4.28

translation

Original

Part 8 - B-Tree leaf Node Format

我们即将把 table 的结构从存储 row 的无序数组转变为 B-Tree,这是一个相当大的改变以至于需要好几章来实现.在本章的末尾，我们将会定义叶子节点的布局，以及支持向只有一个节点的树中插入键值对.

不过首先让我们回想一下为什么转换到树结构.

Alternative Table Formats

基于目前的存储格式，每页只存储 row(没有元数据)因此空间利用效率很高.插入也很快因为我们只需要插入到末尾.但是寻找指定的 row 只能通过遍历整个 table 来完成,并且如果我们想要删除 row,我们需要将删除的 row 之后的所有行前移以填补空缺.

如果我们以数组的形式存储 table,但是 row 通过 id 排序,我们可以使用二分查找指定的 id.但是插入操作会非常耗时，因为我们要移动很多行以腾出空间.

因此，我们将使用 tree 结构.树中的每一個节点可以包含可变数量的行,所以我们需要在节点中存储一些信息以表示它包含了多少行.此外还有不存储任何行的内部节点的空间开销.作为数据库文件变大的交换，我们得到了快速插入，删除和查找.

	存储 row 的无序数组	存储 row 的有序数组	树的节点
page 存储的数据	仅数据	仅数据	元数据，主键值和数据
每页的行数	more	more	fewer
插入	O(1)	O(n)	O(log(n))
删除	O(n)	O(n)	O(log(n))
通过 id 查找	O(n)	O(log(n))	O(log(n))

内部节点和叶子节点拥有不同的布局，让我们定义一个枚举变量表示节点的类型.

//+typedef enum { NODE_INTERNAL, NODE_LEAF } NodeType;
// 译者注: 因为下文要求type大小为1字节，所以制定了enum大小为uint8_t,否则默认为4个字节
typedef enum : uint8_t
{
    NODE_INTERNAL,
    NODE_LEAF
} NodeType;

每一个节点对应着一页.内部节点存储着指向子节点的指针，该指针实际上是存储着该子节点的页的 page number(译者注:即下标).btree 向 pager 请求指定的 page number,pager 返回指向该页缓存的指针.页根据 page number 有序存储在数据库文件中.

节点需要在页的头部存储一些元数据.每个节点会存储它的类型,是否为根节点，和一个指向父节点的指针(用来寻找兄弟节点).我定义了常量来表示头部的每个字段的大小和偏移量.

+/*
+ * Common Node Header Layout
+ */
+const uint32_t NODE_TYPE_SIZE = sizeof(NodeType);
+const uint32_t NODE_TYPE_OFFSET = 0;
+const uint32_t IS_ROOT_SIZE = sizeof(uint8_t);
+const uint32_t IS_ROOT_OFFSET = NODE_TYPE_SIZE;
+const uint32_t PARENT_POINTER_SIZE = sizeof(uint32_t);
+const uint32_t PARENT_POINTER_OFFSET = IS_ROOT_OFFSET + IS_ROOT_SIZE;
+const uint8_t COMMON_NODE_HEADER_SIZE =
+    NODE_TYPE_SIZE + IS_ROOT_SIZE + PARENT_POINTER_SIZE;

Leaf Node Format

除了这些通用的头部字段外，叶子节点需要存储包含的”cell”的数量.一个”cell”就是一个键值对.

+/*
+ * Leaf Node Header Layout
+ */
+const uint32_t LEAF_NODE_NUM_CELLS_SIZE = sizeof(uint32_t);
+const uint32_t LEAF_NODE_NUM_CELLS_OFFSET = COMMON_NODE_HEADER_SIZE;
+const uint32_t LEAF_NODE_HEADER_SIZE =
+    COMMON_NODE_HEADER_SIZE + LEAF_NODE_NUM_CELLS_SIZE;

叶子节点的 body 是 cell 数组.每个 cell 是一个键后面跟着一个值(一个序列化的行).

+/*
+ * Leaf Node Body Layout
+ */
+const uint32_t LEAF_NODE_KEY_SIZE = sizeof(uint32_t);
+const uint32_t LEAF_NODE_KEY_OFFSET = 0;
+const uint32_t LEAF_NODE_VALUE_SIZE = ROW_SIZE;
+const uint32_t LEAF_NODE_VALUE_OFFSET =
+    LEAF_NODE_KEY_OFFSET + LEAF_NODE_KEY_SIZE;
+const uint32_t LEAF_NODE_CELL_SIZE = LEAF_NODE_KEY_SIZE + LEAF_NODE_VALUE_SIZE;
+const uint32_t LEAF_NODE_SPACE_FOR_CELLS = PAGE_SIZE - LEAF_NODE_HEADER_SIZE;
+const uint32_t LEAF_NODE_MAX_CELLS =
+    LEAF_NODE_SPACE_FOR_CELLS / LEAF_NODE_CELL_SIZE;

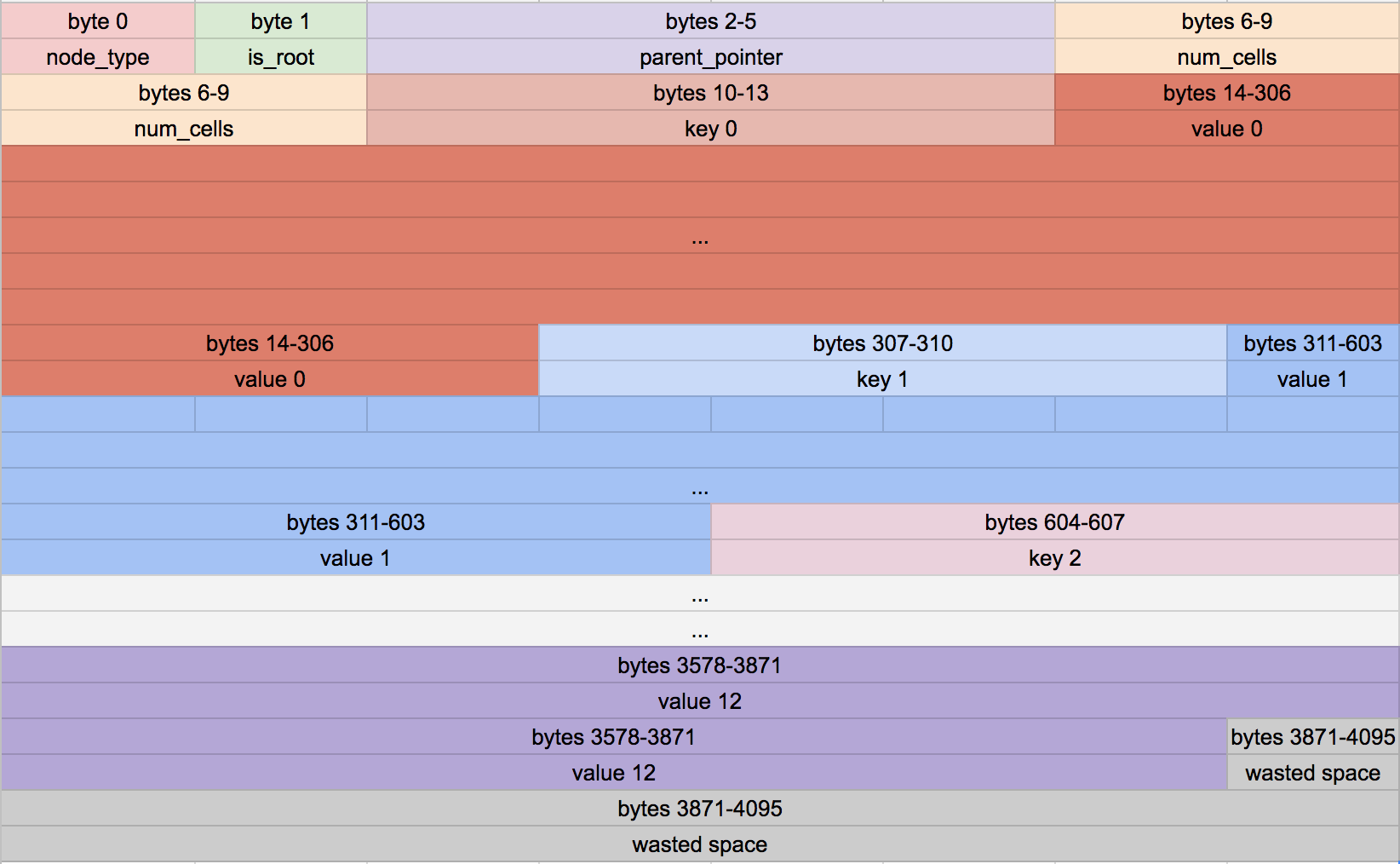
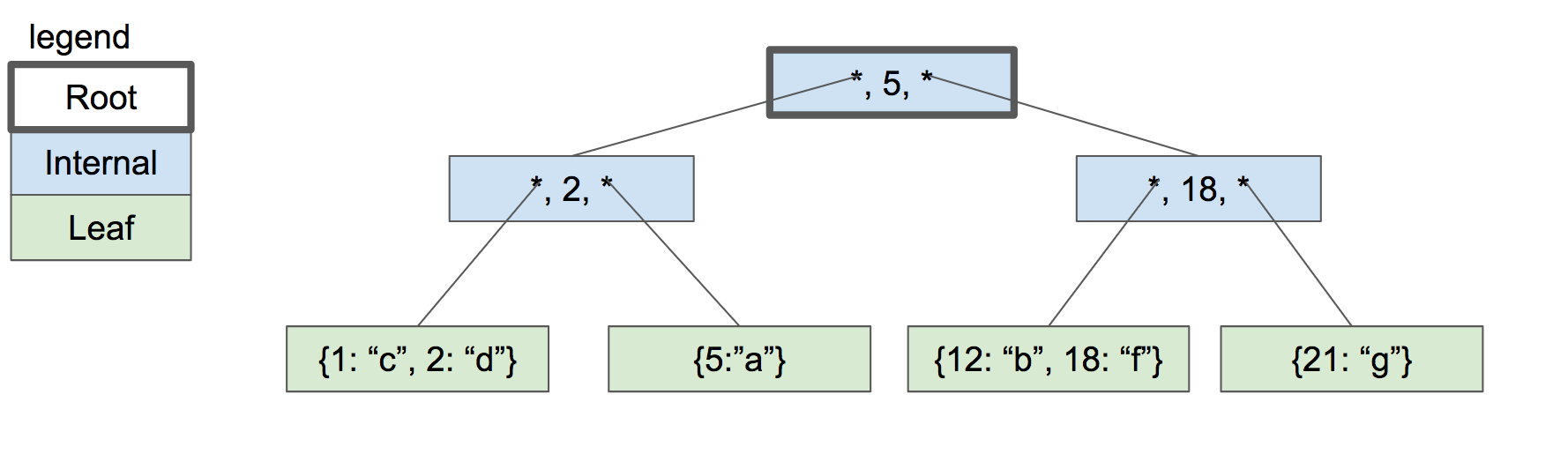
基于这些常量,这里是叶子节点目前布局:

Our leaf node format

在头部使用一整个字节表示一个 bool 值有点浪费空间，但是这会让通过代码获取这些值更容易一点.

还要注意末尾有一些被浪费的空间.我们在头部之后存储尽可能多的 cell,但是剩余的空间不能存储一整个 cell.我们不使用这片空间以避免把 cell 分割到两个节点.

Accessing Leaf Node Fields

获取键，值和元数据的函数都涉及到使用我们刚刚定义的常量进行指针算数运算.

+uint32_t* leaf_node_num_cells(void* node) {
+  return node + LEAF_NODE_NUM_CELLS_OFFSET;
+}
+
+void* leaf_node_cell(void* node, uint32_t cell_num) {
+  return node + LEAF_NODE_HEADER_SIZE + cell_num * LEAF_NODE_CELL_SIZE;
+}
+
+uint32_t* leaf_node_key(void* node, uint32_t cell_num) {
+  return leaf_node_cell(node, cell_num);
+}
+
+void* leaf_node_value(void* node, uint32_t cell_num) {
+  return leaf_node_cell(node, cell_num) + LEAF_NODE_KEY_SIZE;
+}
+
+void initialize_leaf_node(void* node) { *leaf_node_num_cells(node) = 0; }
+

每个节点将确切地占据一页，即使页没满.这意味着我们的 pager 不再需要支持读/写未满的页了.

-void pager_flush(Pager* pager, uint32_t page_num, uint32_t size) {
+void pager_flush(Pager* pager, uint32_t page_num) {
   if (pager->pages[page_num] == NULL) {
     printf("Tried to flush null page\n");
     exit(EXIT_FAILURE);
@@ -242,7 +337,7 @@ void pager_flush(Pager* pager, uint32_t page_num, uint32_t size) {
   }

   ssize_t bytes_written =
-      write(pager->file_descriptor, pager->pages[page_num], size);
+      write(pager->file_descriptor, pager->pages[page_num], PAGE_SIZE);

   if (bytes_written == -1) {
     printf("Error writing: %d\n", errno);

 void db_close(Table* table) {
   Pager* pager = table->pager;
-  uint32_t num_full_pages = table->num_rows / ROWS_PER_PAGE;

-  for (uint32_t i = 0; i < num_full_pages; i++) {
+  for (uint32_t i = 0; i < pager->num_pages; i++) {
     if (pager->pages[i] == NULL) {
       continue;
     }
-    pager_flush(pager, i, PAGE_SIZE);
+    pager_flush(pager, i);
     free(pager->pages[i]);
     pager->pages[i] = NULL;
   }

-  // There may be a partial page to write to the end of the file
-  // This should not be needed after we switch to a B-tree
-  uint32_t num_additional_rows = table->num_rows % ROWS_PER_PAGE;
-  if (num_additional_rows > 0) {
-    uint32_t page_num = num_full_pages;
-    if (pager->pages[page_num] != NULL) {
-      pager_flush(pager, page_num, num_additional_rows * ROW_SIZE);
-      free(pager->pages[page_num]);
-      pager->pages[page_num] = NULL;
-    }
-  }
-
   int result = close(pager->file_descriptor);
   if (result == -1) {
     printf("Error closing db file.\n");

现在更明智的做法是在数据库中存储 page 的个数而不是 row 的个数.page 的个数和 pager 对象关联，而不是 table,因为这是被数据库使用的 page 的个数，而不是指定的 table.一个 btree 被它的根节点对应的 page 下标标识，所以 table 对象需要保存该下标.

 const uint32_t PAGE_SIZE = 4096;
 const uint32_t TABLE_MAX_PAGES = 100;
-const uint32_t ROWS_PER_PAGE = PAGE_SIZE / ROW_SIZE;
-const uint32_t TABLE_MAX_ROWS = ROWS_PER_PAGE * TABLE_MAX_PAGES;

 typedef struct {
   int file_descriptor;
   uint32_t file_length;
+  uint32_t num_pages;
   void* pages[TABLE_MAX_PAGES];
 } Pager;

 typedef struct {
   Pager* pager;
-  uint32_t num_rows;
+  uint32_t root_page_num;
 } Table;

@@ -127,6 +200,10 @@ void* get_page(Pager* pager, uint32_t page_num) {
     }

     pager->pages[page_num] = page;
+
+    if (page_num >= pager->num_pages) {
+      pager->num_pages = page_num + 1;
+    }
   }

   return pager->pages[page_num];

@@ -184,6 +269,12 @@ Pager* pager_open(const char* filename) {
   Pager* pager = malloc(sizeof(Pager));
   pager->file_descriptor = fd;
   pager->file_length = file_length;
+  pager->num_pages = (file_length / PAGE_SIZE);
+
+  if (file_length % PAGE_SIZE != 0) {
+    printf("Db file is not a whole number of pages. Corrupt file.\n");
+    exit(EXIT_FAILURE);
+  }

   for (uint32_t i = 0; i < TABLE_MAX_PAGES; i++) {
     pager->pages[i] = NULL;

Changes to the Cursor Object

cursor 对象表示在 table 中的位置,当我们的 table 只是一个简单的元素为 row 的数组,我们只需要给定 row number 就可以访问该行.现在它是一棵树,我们通过 page number 和 cell 在节点中的 cell number 来标识一个位置.

 typedef struct {
   Table* table;
-  uint32_t row_num;
+  uint32_t page_num;
+  uint32_t cell_num;
   bool end_of_table;  // Indicates a position one past the last element
 } Cursor;

 Cursor* table_start(Table* table) {
   Cursor* cursor = malloc(sizeof(Cursor));
   cursor->table = table;
-  cursor->row_num = 0;
-  cursor->end_of_table = (table->num_rows == 0);
+  cursor->page_num = table->root_page_num;
+  cursor->cell_num = 0;
+
+  void* root_node = get_page(table->pager, table->root_page_num);
+  uint32_t num_cells = *leaf_node_num_cells(root_node);
+  cursor->end_of_table = (num_cells == 0);

   return cursor;
 }

 Cursor* table_end(Table* table) {
   Cursor* cursor = malloc(sizeof(Cursor));
   cursor->table = table;
-  cursor->row_num = table->num_rows;
+  cursor->page_num = table->root_page_num;
+
+  void* root_node = get_page(table->pager, table->root_page_num);
+  uint32_t num_cells = *leaf_node_num_cells(root_node);
+  cursor->cell_num = num_cells;
   cursor->end_of_table = true;

   return cursor;
 }

 void* cursor_value(Cursor* cursor) {
-  uint32_t row_num = cursor->row_num;
-  uint32_t page_num = row_num / ROWS_PER_PAGE;
+  uint32_t page_num = cursor->page_num;
   void* page = get_page(cursor->table->pager, page_num);
-  uint32_t row_offset = row_num % ROWS_PER_PAGE;
-  uint32_t byte_offset = row_offset * ROW_SIZE;
-  return page + byte_offset;
+  return leaf_node_value(page, cursor->cell_num);
 }

 void cursor_advance(Cursor* cursor) {
-  cursor->row_num += 1;
-  if (cursor->row_num >= cursor->table->num_rows) {
+  uint32_t page_num = cursor->page_num;
+  void* node = get_page(cursor->table->pager, page_num);
+
+  cursor->cell_num += 1;
+  if (cursor->cell_num >= (*leaf_node_num_cells(node))) {
     cursor->end_of_table = true;
   }
 }

Insertion Into a Leaf Node

在本章我们会实现一个只有一个节点的树.回忆一下上一章的一开始只有一个空的叶子节点的树:

empty btree

键值对可以一直放入，直到叶子节点被填满:

当我们第一次打开数据库，数据库文件是空的，所以我们初始化 page 0 为一个空的叶子节点(也是根节点):

 Table* db_open(const char* filename) {
   Pager* pager = pager_open(filename);
-  uint32_t num_rows = pager->file_length / ROW_SIZE;

   Table* table = malloc(sizeof(Table));
   table->pager = pager;
-  table->num_rows = num_rows;
+  table->root_page_num = 0;
+
+  if (pager->num_pages == 0) {
+    // New database file. Initialize page 0 as leaf node.
+    void* root_node = get_page(pager, 0);
+    initialize_leaf_node(root_node);
+  }

   return table;
 }

然后我们会创建一个用来向叶子节点中插入键值对的函数,函数的参数 cursor 包含键值对应该被插入的位置.

+void leaf_node_insert(Cursor* cursor, uint32_t key, Row* value) {
+  void* node = get_page(cursor->table->pager, cursor->page_num);
+
+  uint32_t num_cells = *leaf_node_num_cells(node);
+  if (num_cells >= LEAF_NODE_MAX_CELLS) {
+    // Node full
+    printf("Need to implement splitting a leaf node.\n");
+    exit(EXIT_FAILURE);
+  }
+
+  if (cursor->cell_num < num_cells) {
+    // Make room for new cell
+    for (uint32_t i = num_cells; i > cursor->cell_num; i--) {
+      memcpy(leaf_node_cell(node, i), leaf_node_cell(node, i - 1),
+             LEAF_NODE_CELL_SIZE);
+    }
+  }
+
+  *(leaf_node_num_cells(node)) += 1;
+  *(leaf_node_key(node, cursor->cell_num)) = key;
+  serialize_row(value, leaf_node_value(node, cursor->cell_num));
+}
+

我们现在还没有实现分裂操作,所以如果 node 容量满了会退出程序.然后将插入位置后面的 cell 右移一位以给新的 cell 腾出空间，然后我们向空的空间写入 key&value.

既然我们假设树只有一个节点，execute_insert()函数只需要调用这个辅助函数:

 ExecuteResult execute_insert(Statement* statement, Table* table) {
-  if (table->num_rows >= TABLE_MAX_ROWS) {
+  void* node = get_page(table->pager, table->root_page_num);
+  if ((*leaf_node_num_cells(node) >= LEAF_NODE_MAX_CELLS)) {
     return EXECUTE_TABLE_FULL;
   }

   Row* row_to_insert = &(statement->row_to_insert);
   Cursor* cursor = table_end(table);

-  serialize_row(row_to_insert, cursor_value(cursor));
-  table->num_rows += 1;
+  leaf_node_insert(cursor, row_to_insert->id, row_to_insert);

   free(cursor);

通过这些改动，我们的数据库就能和之前一样工作了!除了现在它会更早地返回”Table 已满”错误，因为我们还不能分裂根节点.

叶子节点可以保存多少行呢?

Command to Print Constants

我增加了一个新的元命令，用来打印一些有趣的常量.

+void print_constants() {
+  printf("ROW_SIZE: %d\n", ROW_SIZE);
+  printf("COMMON_NODE_HEADER_SIZE: %d\n", COMMON_NODE_HEADER_SIZE);
+  printf("LEAF_NODE_HEADER_SIZE: %d\n", LEAF_NODE_HEADER_SIZE);
+  printf("LEAF_NODE_CELL_SIZE: %d\n", LEAF_NODE_CELL_SIZE);
+  printf("LEAF_NODE_SPACE_FOR_CELLS: %d\n", LEAF_NODE_SPACE_FOR_CELLS);
+  printf("LEAF_NODE_MAX_CELLS: %d\n", LEAF_NODE_MAX_CELLS);
+}
+
@@ -294,6 +376,14 @@ MetaCommandResult do_meta_command(InputBuffer* input_buffer, Table* table) {
   if (strcmp(input_buffer->buffer, ".exit") == 0) {
     db_close(table);
     exit(EXIT_SUCCESS);
+  } else if (strcmp(input_buffer->buffer, ".constants") == 0) {
+    printf("Constants:\n");
+    print_constants();
+    return META_COMMAND_SUCCESS;
   } else {
     return META_COMMAND_UNRECOGNIZED_COMMAND;
   }

我还添加了一个测试，可以用来提醒我们这些变量改变了:

+  it 'prints constants' do
+    script = [
+      ".constants",
+      ".exit",
+    ]
+    result = run_script(script)
+
+    expect(result).to match_array([
+      "db > Constants:",
+      "ROW_SIZE: 293",
+      "COMMON_NODE_HEADER_SIZE: 6",
+      "LEAF_NODE_HEADER_SIZE: 10",
+      "LEAF_NODE_CELL_SIZE: 297",
+      "LEAF_NODE_SPACE_FOR_CELLS: 4086",
+      "LEAF_NODE_MAX_CELLS: 13",
+      "db > ",
+    ])
+  end

现在我们的 table 可以保存 13 行喔!

Tree Visualization

为了便于调试和可视化,我还增加了一个元命令来打印出 btree 表现形式.

+void print_leaf_node(void* node) {
+  uint32_t num_cells = *leaf_node_num_cells(node);
+  printf("leaf (size %d)\n", num_cells);
+  for (uint32_t i = 0; i < num_cells; i++) {
+    uint32_t key = *leaf_node_key(node, i);
+    printf("  - %d : %d\n", i, key);
+  }
+}
+

@@ -294,6 +376,14 @@ MetaCommandResult do_meta_command(InputBuffer* input_buffer, Table* table) {
   if (strcmp(input_buffer->buffer, ".exit") == 0) {
     db_close(table);
     exit(EXIT_SUCCESS);
+  } else if (strcmp(input_buffer->buffer, ".btree") == 0) {
+    printf("Tree:\n");
+    print_leaf_node(get_page(table->pager, 0));
+    return META_COMMAND_SUCCESS;
   } else if (strcmp(input_buffer->buffer, ".constants") == 0) {
     printf("Constants:\n");
     print_constants();
     return META_COMMAND_SUCCESS;
   } else {
     return META_COMMAND_UNRECOGNIZED_COMMAND;
   }

以及一个测试

+  it 'allows printing out the structure of a one-node btree' do
+    script = [3, 1, 2].map do |i|
+      "insert #{i} user#{i} person#{i}@example.com"
+    end
+    script << ".btree"
+    script << ".exit"
+    result = run_script(script)
+
+    expect(result).to match_array([
+      "db > Executed.",
+      "db > Executed.",
+      "db > Executed.",
+      "db > Tree:",
+      "leaf (size 3)",
+      "  - 0 : 3",
+      "  - 1 : 1",
+      "  - 2 : 2",
+      "db > "
+    ])
+  end

果咩，我们仍然没能有序地存储行.你可能注意到了execute_insert()函数在叶子节点的插入位置是由函数table_end()返回的.所以行是以插入的顺序排序的,就像之前一样.

Next Time

本章看起来像是倒退了一步.我们的数据库现在存储的行比之前少，并且我们存储的行仍然是无序的.但就像我在一开始说的，这是我们的一大步，并且将其分解成可管理的步骤很重要.

下一章，我们会实现根据 primary key(主键值)查找记录，然后有序地存储行.

Complete Diff

@@ -62,29 +62,101 @@ const uint32_t ROW_SIZE = ID_SIZE + USERNAME_SIZE + EMAIL_SIZE;

 const uint32_t PAGE_SIZE = 4096;
 #define TABLE_MAX_PAGES 100
-const uint32_t ROWS_PER_PAGE = PAGE_SIZE / ROW_SIZE;
-const uint32_t TABLE_MAX_ROWS = ROWS_PER_PAGE * TABLE_MAX_PAGES;

 typedef struct {
   int file_descriptor;
   uint32_t file_length;
+  uint32_t num_pages;
   void* pages[TABLE_MAX_PAGES];
 } Pager;

 typedef struct {
   Pager* pager;
-  uint32_t num_rows;
+  uint32_t root_page_num;
 } Table;

 typedef struct {
   Table* table;
-  uint32_t row_num;
+  uint32_t page_num;
+  uint32_t cell_num;
   bool end_of_table;  // Indicates a position one past the last element
 } Cursor;

+typedef enum { NODE_INTERNAL, NODE_LEAF } NodeType;
+
+/*
+ * Common Node Header Layout
+ */
+const uint32_t NODE_TYPE_SIZE = sizeof(uint8_t);
+const uint32_t NODE_TYPE_OFFSET = 0;
+const uint32_t IS_ROOT_SIZE = sizeof(uint8_t);
+const uint32_t IS_ROOT_OFFSET = NODE_TYPE_SIZE;
+const uint32_t PARENT_POINTER_SIZE = sizeof(uint32_t);
+const uint32_t PARENT_POINTER_OFFSET = IS_ROOT_OFFSET + IS_ROOT_SIZE;
+const uint8_t COMMON_NODE_HEADER_SIZE =
+    NODE_TYPE_SIZE + IS_ROOT_SIZE + PARENT_POINTER_SIZE;
+
+/*
+ * Leaf Node Header Layout
+ */
+const uint32_t LEAF_NODE_NUM_CELLS_SIZE = sizeof(uint32_t);
+const uint32_t LEAF_NODE_NUM_CELLS_OFFSET = COMMON_NODE_HEADER_SIZE;
+const uint32_t LEAF_NODE_HEADER_SIZE =
+    COMMON_NODE_HEADER_SIZE + LEAF_NODE_NUM_CELLS_SIZE;
+
+/*
+ * Leaf Node Body Layout
+ */
+const uint32_t LEAF_NODE_KEY_SIZE = sizeof(uint32_t);
+const uint32_t LEAF_NODE_KEY_OFFSET = 0;
+const uint32_t LEAF_NODE_VALUE_SIZE = ROW_SIZE;
+const uint32_t LEAF_NODE_VALUE_OFFSET =
+    LEAF_NODE_KEY_OFFSET + LEAF_NODE_KEY_SIZE;
+const uint32_t LEAF_NODE_CELL_SIZE = LEAF_NODE_KEY_SIZE + LEAF_NODE_VALUE_SIZE;
+const uint32_t LEAF_NODE_SPACE_FOR_CELLS = PAGE_SIZE - LEAF_NODE_HEADER_SIZE;
+const uint32_t LEAF_NODE_MAX_CELLS =
+    LEAF_NODE_SPACE_FOR_CELLS / LEAF_NODE_CELL_SIZE;
+
+uint32_t* leaf_node_num_cells(void* node) {
+  return node + LEAF_NODE_NUM_CELLS_OFFSET;
+}
+
+void* leaf_node_cell(void* node, uint32_t cell_num) {
+  return node + LEAF_NODE_HEADER_SIZE + cell_num * LEAF_NODE_CELL_SIZE;
+}
+
+uint32_t* leaf_node_key(void* node, uint32_t cell_num) {
+  return leaf_node_cell(node, cell_num);
+}
+
+void* leaf_node_value(void* node, uint32_t cell_num) {
+  return leaf_node_cell(node, cell_num) + LEAF_NODE_KEY_SIZE;
+}
+
+void print_constants() {
+  printf("ROW_SIZE: %d\n", ROW_SIZE);
+  printf("COMMON_NODE_HEADER_SIZE: %d\n", COMMON_NODE_HEADER_SIZE);
+  printf("LEAF_NODE_HEADER_SIZE: %d\n", LEAF_NODE_HEADER_SIZE);
+  printf("LEAF_NODE_CELL_SIZE: %d\n", LEAF_NODE_CELL_SIZE);
+  printf("LEAF_NODE_SPACE_FOR_CELLS: %d\n", LEAF_NODE_SPACE_FOR_CELLS);
+  printf("LEAF_NODE_MAX_CELLS: %d\n", LEAF_NODE_MAX_CELLS);
+}
+
+void print_leaf_node(void* node) {
+  uint32_t num_cells = *leaf_node_num_cells(node);
+  printf("leaf (size %d)\n", num_cells);
+  for (uint32_t i = 0; i < num_cells; i++) {
+    uint32_t key = *leaf_node_key(node, i);
+    printf("  - %d : %d\n", i, key);
+  }
+}
+
 void print_row(Row* row) {
     printf("(%d, %s, %s)\n", row->id, row->username, row->email);
 }
@@ -101,6 +173,8 @@ void deserialize_row(void *source, Row* destination) {
     memcpy(&(destination->email), source + EMAIL_OFFSET, EMAIL_SIZE);
 }

+void initialize_leaf_node(void* node) { *leaf_node_num_cells(node) = 0; }
+
 void* get_page(Pager* pager, uint32_t page_num) {
   if (page_num > TABLE_MAX_PAGES) {
     printf("Tried to fetch page number out of bounds. %d > %d\n", page_num,
@@ -128,6 +202,10 @@ void* get_page(Pager* pager, uint32_t page_num) {
     }

     pager->pages[page_num] = page;
+
+    if (page_num >= pager->num_pages) {
+      pager->num_pages = page_num + 1;
+    }
   }

   return pager->pages[page_num];
@@ -136,8 +214,12 @@ void* get_page(Pager* pager, uint32_t page_num) {
 Cursor* table_start(Table* table) {
   Cursor* cursor = malloc(sizeof(Cursor));
   cursor->table = table;
-  cursor->row_num = 0;
-  cursor->end_of_table = (table->num_rows == 0);
+  cursor->page_num = table->root_page_num;
+  cursor->cell_num = 0;
+
+  void* root_node = get_page(table->pager, table->root_page_num);
+  uint32_t num_cells = *leaf_node_num_cells(root_node);
+  cursor->end_of_table = (num_cells == 0);

   return cursor;
 }
@@ -145,24 +227,28 @@ Cursor* table_start(Table* table) {
 Cursor* table_end(Table* table) {
   Cursor* cursor = malloc(sizeof(Cursor));
   cursor->table = table;
-  cursor->row_num = table->num_rows;
+  cursor->page_num = table->root_page_num;
+
+  void* root_node = get_page(table->pager, table->root_page_num);
+  uint32_t num_cells = *leaf_node_num_cells(root_node);
+  cursor->cell_num = num_cells;
   cursor->end_of_table = true;

   return cursor;
 }

 void* cursor_value(Cursor* cursor) {
-  uint32_t row_num = cursor->row_num;
-  uint32_t page_num = row_num / ROWS_PER_PAGE;
+  uint32_t page_num = cursor->page_num;
   void* page = get_page(cursor->table->pager, page_num);
-  uint32_t row_offset = row_num % ROWS_PER_PAGE;
-  uint32_t byte_offset = row_offset * ROW_SIZE;
-  return page + byte_offset;
+  return leaf_node_value(page, cursor->cell_num);
 }

 void cursor_advance(Cursor* cursor) {
-  cursor->row_num += 1;
-  if (cursor->row_num >= cursor->table->num_rows) {
+  uint32_t page_num = cursor->page_num;
+  void* node = get_page(cursor->table->pager, page_num);
+
+  cursor->cell_num += 1;
+  if (cursor->cell_num >= (*leaf_node_num_cells(node))) {
     cursor->end_of_table = true;
   }
 }
@@ -185,6 +271,12 @@ Pager* pager_open(const char* filename) {
   Pager* pager = malloc(sizeof(Pager));
   pager->file_descriptor = fd;
   pager->file_length = file_length;
+  pager->num_pages = (file_length / PAGE_SIZE);
+
+  if (file_length % PAGE_SIZE != 0) {
+    printf("Db file is not a whole number of pages. Corrupt file.\n");
+    exit(EXIT_FAILURE);
+  }

   for (uint32_t i = 0; i < TABLE_MAX_PAGES; i++) {
     pager->pages[i] = NULL;
@@ -194,11 +285,15 @@ Pager* pager_open(const char* filename) {
@@ -195,11 +287,16 @@ Pager* pager_open(const char* filename) {

 Table* db_open(const char* filename) {
   Pager* pager = pager_open(filename);
-  uint32_t num_rows = pager->file_length / ROW_SIZE;

   Table* table = malloc(sizeof(Table));
   table->pager = pager;
-  table->num_rows = num_rows;
+  table->root_page_num = 0;
+
+  if (pager->num_pages == 0) {
+    // New database file. Initialize page 0 as leaf node.
+    void* root_node = get_page(pager, 0);
+    initialize_leaf_node(root_node);
+  }

   return table;
 }
@@ -234,7 +331,7 @@ void close_input_buffer(InputBuffer* input_buffer) {
     free(input_buffer);
 }

-void pager_flush(Pager* pager, uint32_t page_num, uint32_t size) {
+void pager_flush(Pager* pager, uint32_t page_num) {
   if (pager->pages[page_num] == NULL) {
     printf("Tried to flush null page\n");
     exit(EXIT_FAILURE);
@@ -242,7 +337,7 @@ void pager_flush(Pager* pager, uint32_t page_num, uint32_t size) {
@@ -249,7 +346,7 @@ void pager_flush(Pager* pager, uint32_t page_num, uint32_t size) {
   }

   ssize_t bytes_written =
-      write(pager->file_descriptor, pager->pages[page_num], size);
+      write(pager->file_descriptor, pager->pages[page_num], PAGE_SIZE);

   if (bytes_written == -1) {
     printf("Error writing: %d\n", errno);
@@ -252,29 +347,16 @@ void pager_flush(Pager* pager, uint32_t page_num, uint32_t size) {
@@ -260,29 +357,16 @@ void pager_flush(Pager* pager, uint32_t page_num, uint32_t size) {

 void db_close(Table* table) {
   Pager* pager = table->pager;
-  uint32_t num_full_pages = table->num_rows / ROWS_PER_PAGE;

-  for (uint32_t i = 0; i < num_full_pages; i++) {
+  for (uint32_t i = 0; i < pager->num_pages; i++) {
     if (pager->pages[i] == NULL) {
       continue;
     }
-    pager_flush(pager, i, PAGE_SIZE);
+    pager_flush(pager, i);
     free(pager->pages[i]);
     pager->pages[i] = NULL;
   }

-  // There may be a partial page to write to the end of the file
-  // This should not be needed after we switch to a B-tree
-  uint32_t num_additional_rows = table->num_rows % ROWS_PER_PAGE;
-  if (num_additional_rows > 0) {
-    uint32_t page_num = num_full_pages;
-    if (pager->pages[page_num] != NULL) {
-      pager_flush(pager, page_num, num_additional_rows * ROW_SIZE);
-      free(pager->pages[page_num]);
-      pager->pages[page_num] = NULL;
-    }
-  }
-
   int result = close(pager->file_descriptor);
   if (result == -1) {
     printf("Error closing db file.\n");
@@ -305,6 +389,14 @@ MetaCommandResult do_meta_command(InputBuffer* input_buffer, Table *table) {
   if (strcmp(input_buffer->buffer, ".exit") == 0) {
     db_close(table);
     exit(EXIT_SUCCESS);
+  } else if (strcmp(input_buffer->buffer, ".btree") == 0) {
+    printf("Tree:\n");
+    print_leaf_node(get_page(table->pager, 0));
+    return META_COMMAND_SUCCESS;
+  } else if (strcmp(input_buffer->buffer, ".constants") == 0) {
+    printf("Constants:\n");
+    print_constants();
+    return META_COMMAND_SUCCESS;
   } else {
     return META_COMMAND_UNRECOGNIZED_COMMAND;
   }
@@ -354,16 +446,39 @@ PrepareResult prepare_statement(InputBuffer* input_buffer,
   return PREPARE_UNRECOGNIZED_STATEMENT;
 }

+void leaf_node_insert(Cursor* cursor, uint32_t key, Row* value) {
+  void* node = get_page(cursor->table->pager, cursor->page_num);
+
+  uint32_t num_cells = *leaf_node_num_cells(node);
+  if (num_cells >= LEAF_NODE_MAX_CELLS) {
+    // Node full
+    printf("Need to implement splitting a leaf node.\n");
+    exit(EXIT_FAILURE);
+  }
+
+  if (cursor->cell_num < num_cells) {
+    // Make room for new cell
+    for (uint32_t i = num_cells; i > cursor->cell_num; i--) {
+      memcpy(leaf_node_cell(node, i), leaf_node_cell(node, i - 1),
+             LEAF_NODE_CELL_SIZE);
+    }
+  }
+
+  *(leaf_node_num_cells(node)) += 1;
+  *(leaf_node_key(node, cursor->cell_num)) = key;
+  serialize_row(value, leaf_node_value(node, cursor->cell_num));
+}
+
 ExecuteResult execute_insert(Statement* statement, Table* table) {
-  if (table->num_rows >= TABLE_MAX_ROWS) {
+  void* node = get_page(table->pager, table->root_page_num);
+  if ((*leaf_node_num_cells(node) >= LEAF_NODE_MAX_CELLS)) {
     return EXECUTE_TABLE_FULL;
   }

   Row* row_to_insert = &(statement->row_to_insert);
   Cursor* cursor = table_end(table);

-  serialize_row(row_to_insert, cursor_value(cursor));
-  table->num_rows += 1;
+  leaf_node_insert(cursor, row_to_insert->id, row_to_insert);

   free(cursor);

And the specs:

+  it 'allows printing out the structure of a one-node btree' do
+    script = [3, 1, 2].map do |i|
+      "insert #{i} user#{i} person#{i}@example.com"
+    end
+    script << ".btree"
+    script << ".exit"
+    result = run_script(script)
+
+    expect(result).to match_array([
+      "db > Executed.",
+      "db > Executed.",
+      "db > Executed.",
+      "db > Tree:",
+      "leaf (size 3)",
+      "  - 0 : 3",
+      "  - 1 : 1",
+      "  - 2 : 2",
+      "db > "
+    ])
+  end
+
+  it 'prints constants' do
+    script = [
+      ".constants",
+      ".exit",
+    ]
+    result = run_script(script)
+
+    expect(result).to match_array([
+      "db > Constants:",
+      "ROW_SIZE: 293",
+      "COMMON_NODE_HEADER_SIZE: 6",
+      "LEAF_NODE_HEADER_SIZE: 10",
+      "LEAF_NODE_CELL_SIZE: 297",
+      "LEAF_NODE_SPACE_FOR_CELLS: 4086",
+      "LEAF_NODE_MAX_CELLS: 13",
+      "db > ",
+    ])
+  end
 end

Part 9 - Binary Search and Duplicate Keys

在上一章注意到我们仍然存储键的方式仍然是无序的.我们将要修复这个问题，外加检测和拒绝重复的键.

目前，函数execute_insert()总是选择在表的末尾插入，但我们应该在表中搜索合适的插入位置，然后插到那里.如果键值已存在，返回一个错误.

ExecuteResult execute_insert(Statement* statement, Table* table) {
   void* node = get_page(table->pager, table->root_page_num);
-  if ((*leaf_node_num_cells(node) >= LEAF_NODE_MAX_CELLS)) {
+  uint32_t num_cells = (*leaf_node_num_cells(node));
+  if (num_cells >= LEAF_NODE_MAX_CELLS) {
     return EXECUTE_TABLE_FULL;
   }

   Row* row_to_insert = &(statement->row_to_insert);
-  Cursor* cursor = table_end(table);
+  uint32_t key_to_insert = row_to_insert->id;
+  Cursor* cursor = table_find(table, key_to_insert);
+
+  if (cursor->cell_num < num_cells) {
+    uint32_t key_at_index = *leaf_node_key(node, cursor->cell_num);
+    if (key_at_index == key_to_insert) {
+      return EXECUTE_DUPLICATE_KEY;
+    }
+  }

   leaf_node_insert(cursor, row_to_insert->id, row_to_insert);

我们不再需要函数table_end()了.

-Cursor* table_end(Table* table) {
-  Cursor* cursor = malloc(sizeof(Cursor));
-  cursor->table = table;
-  cursor->page_num = table->root_page_num;
-
-  void* root_node = get_page(table->pager, table->root_page_num);
-  uint32_t num_cells = *leaf_node_num_cells(root_node);
-  cursor->cell_num = num_cells;
-  cursor->end_of_table = true;
-
-  return cursor;
-}

我们用一个新函数代替它，该函数可以在树中搜索一个给定的key.

+/*
+Return the position of the given key.
+If the key is not present, return the position
+where it should be inserted
+*/
+Cursor* table_find(Table* table, uint32_t key) {
+  uint32_t root_page_num = table->root_page_num;
+  void* root_node = get_page(table->pager, root_page_num);
+
+  if (get_node_type(root_node) == NODE_LEAF) {
+    return leaf_node_find(table, root_page_num, key);
+  } else {
+    printf("Need to implement searching an internal node\n");
+    exit(EXIT_FAILURE);
+  }
+}

我预留了处理内部节点的分支，尽管我们还没有实现内部节点.不过我们现在可以用二分查找搜索叶子节点.

+Cursor* leaf_node_find(Table* table, uint32_t page_num, uint32_t key) {
+  void* node = get_page(table->pager, page_num);
+  uint32_t num_cells = *leaf_node_num_cells(node);
+
+  Cursor* cursor = malloc(sizeof(Cursor));
+  cursor->table = table;
+  cursor->page_num = page_num;
+
+  // Binary search
+  uint32_t min_index = 0;
+  uint32_t one_past_max_index = num_cells;
+  while (one_past_max_index != min_index) {
+    uint32_t index = (min_index + one_past_max_index) / 2;
+    uint32_t key_at_index = *leaf_node_key(node, index);
+    if (key == key_at_index) {
+      cursor->cell_num = index;
+      return cursor;
+    }
+    if (key < key_at_index) {
+      one_past_max_index = index;
+    } else {
+      min_index = index + 1;
+    }
+  }
+
+  cursor->cell_num = min_index;
+  return cursor;
+}

该函数的返回值为:

键对应的位置
另一个键的位置，如果我们想要插入新的键的话，就需要移动它，或者
最后一个键的后一个位置

因为我们现在需要检查节点类型，所以需要一个函数去获得和设置类型值.

+NodeType get_node_type(void* node) {
+  uint8_t value = *((uint8_t*)(node + NODE_TYPE_OFFSET));
+  return (NodeType)value;
+}
+
+void set_node_type(void* node, NodeType type) {
+  uint8_t value = type;
+  *((uint8_t*)(node + NODE_TYPE_OFFSET)) = value;
+}

我们需要先转换到unt8_t类型以确保其被序列化为一个字节.

我们还需要初始化节点类型.

-void initialize_leaf_node(void* node) { *leaf_node_num_cells(node) = 0; }
+void initialize_leaf_node(void* node) {
+  set_node_type(node, NODE_LEAF);
+  *leaf_node_num_cells(node) = 0;
+}

最后，我们需要创建和处理一个新的错误码.

-enum ExecuteResult_t { EXECUTE_SUCCESS, EXECUTE_TABLE_FULL };
+enum ExecuteResult_t {
+  EXECUTE_SUCCESS,
+  EXECUTE_DUPLICATE_KEY,
+  EXECUTE_TABLE_FULL
+};

       case (EXECUTE_SUCCESS):
         printf("Executed.\n");
         break;
+      case (EXECUTE_DUPLICATE_KEY):
+        printf("Error: Duplicate key.\n");
+        break;
       case (EXECUTE_TABLE_FULL):
         printf("Error: Table full.\n");
         break;

通过这些改动，我们的测试可以改为检查顺序.

       "db > Executed.",
       "db > Tree:",
       "leaf (size 3)",
-      "  - 0 : 3",
-      "  - 1 : 1",
-      "  - 2 : 2",
+      "  - 0 : 1",
+      "  - 1 : 2",
+      "  - 2 : 3",
       "db > "
     ])
   end

然后我们可以新增一个检查重复键的测试:

+  it 'prints an error message if there is a duplicate id' do
+    script = [
+      "insert 1 user1 person1@example.com",
+      "insert 1 user1 person1@example.com",
+      "select",
+      ".exit",
+    ]
+    result = run_script(script)
+    expect(result).to match_array([
+      "db > Executed.",
+      "db > Error: Duplicate key.",
+      "db > (1, user1, person1@example.com)",
+      "Executed.",
+      "db > ",
+    ])
+  end

好辣!在下一章我们将会 - 实施分裂叶子节点并且创建内部节点.

Part 10 - Splitting a Leaf Node

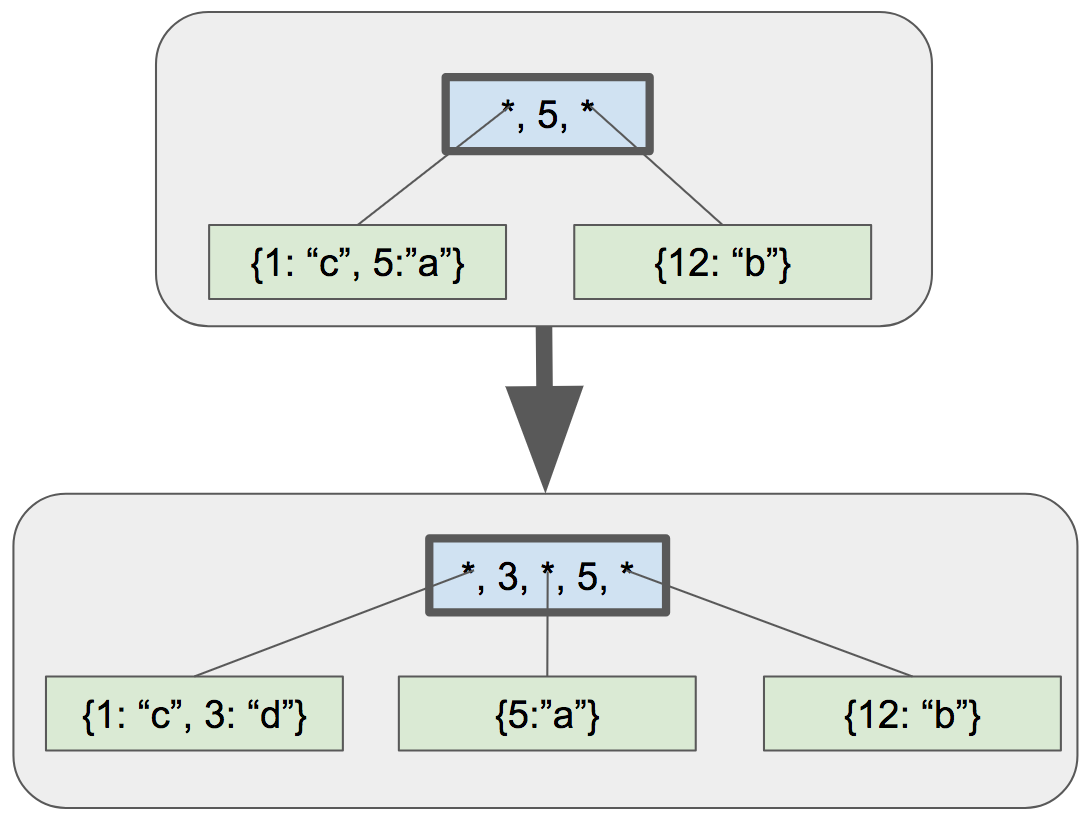
我们的B-Tree不太像一个树，因为只有一个节点.为了修复这个问题，我们需要一些代码来将一个叶子节点分裂成双胞胎.在这之后,我们需要创建一个内部节点作为两个叶子节点的父节点.

本章目标基本上是从这样:

到这样:

two-level btree

首先让我们移除叶子节点已满的错误处理:

 void leaf_node_insert(Cursor* cursor, uint32_t key, Row* value) {
   void* node = get_page(cursor->table->pager, cursor->page_num);
 
   uint32_t num_cells = *leaf_node_num_cells(node);
   if (num_cells >= LEAF_NODE_MAX_CELLS) {
     // Node full
-    printf("Need to implement splitting a leaf node.\n");
-    exit(EXIT_FAILURE);
+    leaf_node_split_and_insert(cursor, key, value);
+    return;
   }

ExecuteResult execute_insert(Statement* statement, Table* table) {
   void* node = get_page(table->pager, table->root_page_num);
   uint32_t num_cells = (*leaf_node_num_cells(node));
-  if (num_cells >= LEAF_NODE_MAX_CELLS) {
-    return EXECUTE_TABLE_FULL;
-  }
 
   Row* row_to_insert = &(statement->row_to_insert);
   uint32_t key_to_insert = row_to_insert->id;

Splitting Algorithm

简单的部分结束了,SQLite Database System: Design and Implementation里面描述了我们接下来要做的事情

如果叶子节点没有剩余空间了，我们应该将叶子节点已有的记录和新的记录(待插入的那个)分成两个等长的部分:下半部分和上半部分(上半部分的所有键都严格大于下半部分的键.)然后创建一个新的叶子节点，然后上半部分移动到叶子节点里.

让我们来处理旧的节点然后创建一个新的节点.

+void leaf_node_split_and_insert(Cursor* cursor, uint32_t key, Row* value) {
+  /*
+  Create a new node and move half the cells over.
+  Insert the new value in one of the two nodes.
+  Update parent or create a new parent.
+  */
+
+  void* old_node = get_page(cursor->table->pager, cursor->page_num);
+  uint32_t new_page_num = get_unused_page_num(cursor->table->pager);
+  void* new_node = get_page(cursor->table->pager, new_page_num);
+  initialize_leaf_node(new_node);

然后，拷贝每个cell到新的位置:

+  /*
+  All existing keys plus new key should be divided
+  evenly between old (left) and new (right) nodes.
+  Starting from the right, move each key to correct position.
+  */
+  for (int32_t i = LEAF_NODE_MAX_CELLS; i >= 0; i--) {
+    void* destination_node;
+    if (i >= LEAF_NODE_LEFT_SPLIT_COUNT) {
+      destination_node = new_node;
+    } else {
+      destination_node = old_node;
+    }
+    uint32_t index_within_node = i % LEAF_NODE_LEFT_SPLIT_COUNT;
+    void* destination = leaf_node_cell(destination_node, index_within_node);
+
+    if (i == cursor->cell_num) {
+      serialize_row(value, destination);
+    } else if (i > cursor->cell_num) {
+      memcpy(destination, leaf_node_cell(old_node, i - 1), LEAF_NODE_CELL_SIZE);
+    } else {
+      memcpy(destination, leaf_node_cell(old_node, i), LEAF_NODE_CELL_SIZE);
+    }
+  }

然后我们需要更新两个叶子节点的父节点.如果原节点(即被分裂的叶子节点)是根节点,也就是没有父节点.在这种情况下，创建一个新的根节点作为父节点,目前我们暂时不实现更新父节点的操作:

+  if (is_node_root(old_node)) {
+    return create_new_root(cursor->table, new_page_num);
+  } else {
+    printf("Need to implement updating parent after split\n");
+    exit(EXIT_FAILURE);
+  }
+}

Allocating New Pages

让我们回去定义一些新的函数和常量.当我们创建一个新的叶子节点时，我们把它放进由函数get_ununsed_page_num()指定的页中:

+/*
+Until we start recycling free pages, new pages will always
+go onto the end of the database file
+*/
+uint32_t get_unused_page_num(Pager* pager) { return pager->num_pages; }

目前，我们假设数据库有N页，page下标从0到N-1已被分配.所以我们可以分配下标N给新的页.最终在我们执行了删除操作之后，一些页可能是空的并且它们的页下标未被使用，为了提高效率，我们可以重新分配那些空的页.

Leaf Node Sizes

为了保持树的平衡，我们将cells平均分配到两个新的节点中.如果一个叶子节点可以保存N个cell,那么在分裂中我们需要分配N+1个cell到两个节点中(N个原cell外加一个待插入的新cell).我决定给左边的节点多分配一个cell,如果N+1是奇数的话.

+const uint32_t LEAF_NODE_RIGHT_SPLIT_COUNT = (LEAF_NODE_MAX_CELLS + 1) / 2;
+const uint32_t LEAF_NODE_LEFT_SPLIT_COUNT =
+    (LEAF_NODE_MAX_CELLS + 1) - LEAF_NODE_RIGHT_SPLIT_COUNT;

Creating a New Root

这里SQLite Database System阐释了创建一个新的根节点的过程:

让N变为根节点.首先分配两个节点，叫做L和R.移动N的下半部分元素到L,上半部分元素到R.然后现在N就是空的了.

在N中增加<L,K,R>，K是L中最大的键.第N页也仍然是根节点.注意树的深度增加了1,但是新的树在不违背任何B+tree属性的情况下保持了高度平衡.

目前，我们已经创建了右孩子并且把上半部分元素移入其中.我们的函数将右孩子作为参数，然后分配一个新的页来存储左孩子.

+void create_new_root(Table* table, uint32_t right_child_page_num) {
+  /*
+  Handle splitting the root.
+  Old root copied to new page, becomes left child.
+  Address of right child passed in.
+  Re-initialize root page to contain the new root node.
+  New root node points to two children.
+  */
+
+  void* root = get_page(table->pager, table->root_page_num);
+  void* right_child = get_page(table->pager, right_child_page_num);
+  uint32_t left_child_page_num = get_unused_page_num(table->pager);
+  void* left_child = get_page(table->pager, left_child_page_num);

原根节点的数据被拷贝进了左孩子,然后我们就能重新使用该页作为根节点了.

+  /* Left child has data copied from old root */
+  memcpy(left_child, root, PAGE_SIZE);
+  set_node_root(left_child, false);

最后我们需要将原根节点对应的页初始化为一个新的有两个孩子的内部节点.

+  /* Root node is a new internal node with one key and two children */
+  initialize_internal_node(root);
+  set_node_root(root, true);
+  *internal_node_num_keys(root) = 1;
+  *internal_node_child(root, 0) = left_child_page_num;
+  uint32_t left_child_max_key = get_node_max_key(left_child);
+  *internal_node_key(root, 0) = left_child_max_key;
+  *internal_node_right_child(root) = right_child_page_num;
+}

Internal Node Format

现在我们终于要创建一个内部节点了,我们要先定义它的布局.

内部节点以普通节点头部开始，然后是它包含的键的数量，然后是它的最右边节点的page number.内部节点存储的指向子节点的指针总是比键的数量多一个.那个额外的子节点指针存储在头部.

+/*
+ * Internal Node Header Layout
+ */
+const uint32_t INTERNAL_NODE_NUM_KEYS_SIZE = sizeof(uint32_t);
+const uint32_t INTERNAL_NODE_NUM_KEYS_OFFSET = COMMON_NODE_HEADER_SIZE;
+const uint32_t INTERNAL_NODE_RIGHT_CHILD_SIZE = sizeof(uint32_t);
+const uint32_t INTERNAL_NODE_RIGHT_CHILD_OFFSET =
+    INTERNAL_NODE_NUM_KEYS_OFFSET + INTERNAL_NODE_NUM_KEYS_SIZE;
+const uint32_t INTERNAL_NODE_HEADER_SIZE = COMMON_NODE_HEADER_SIZE +
+                                           INTERNAL_NODE_NUM_KEYS_SIZE +
+                                           INTERNAL_NODE_RIGHT_CHILD_SIZE;

body是一个存储cell的数组，每个cell包含一个指向子节点的指针和键.每个键应该是该键左边的子节点中的最大的键值.

+/*
+ * Internal Node Body Layout
+ */
+const uint32_t INTERNAL_NODE_KEY_SIZE = sizeof(uint32_t);
+const uint32_t INTERNAL_NODE_CHILD_SIZE = sizeof(uint32_t);
+const uint32_t INTERNAL_NODE_CELL_SIZE =
+    INTERNAL_NODE_CHILD_SIZE + INTERNAL_NODE_KEY_SIZE;

基于这些常量,内部节点的布局应该长这样:

Our internal node format

Notice our huge branching factor(不知道咋翻译…).因为每个子节点指针&键组合相当小，每个内部节点可以存储510个键和511个孩子指针.这意味着我们几乎不会需要遍历树的很多层来找到一个给定的键值.

# 内部节点层数	最多 # 叶子节点	所有叶子节点的总大小
0	511^0=1	4KB
1	511^1=512	~ 2MB
2	511^2=261,121	~ 1GB
3	511^3=133,432,831	~ 550GB

实际上，每个叶子节点不可能将4KB全部用来存储数据,因为还需要存储头部信息,键,还有一些空间被浪费了.但是我们只需要从磁盘中加载4页数据就可以搜索500GB的数据.这就是为什么B-Tree这个数据结构非常适合数据库.

这里有一些函数用来想内部节点读写数据:

+uint32_t* internal_node_num_keys(void* node) {
+  return node + INTERNAL_NODE_NUM_KEYS_OFFSET;
+}
+
+uint32_t* internal_node_right_child(void* node) {
+  return node + INTERNAL_NODE_RIGHT_CHILD_OFFSET;
+}
+
+uint32_t* internal_node_cell(void* node, uint32_t cell_num) {
+  return node + INTERNAL_NODE_HEADER_SIZE + cell_num * INTERNAL_NODE_CELL_SIZE;
+}
+
+uint32_t* internal_node_child(void* node, uint32_t child_num) {
+  uint32_t num_keys = *internal_node_num_keys(node);
+  if (child_num > num_keys) {
+    printf("Tried to access child_num %d > num_keys %d\n", child_num, num_keys);
+    exit(EXIT_FAILURE);
+  } else if (child_num == num_keys) {
+    return internal_node_right_child(node);
+  } else {
+    return internal_node_cell(node, child_num);
+  }
+}
+
+uint32_t* internal_node_key(void* node, uint32_t key_num) {
+  return (uint32_t* )((unsigned char* )internal_node_cell(node,key_num)+INTERNAL_NODE_CHILD_SIZE);
+}

译者注: 函数`internal_node_key()`的返回值原文为
return internal_node_cell(node, key_num) + INTERNAL_NODE_CHILD_SIZE;

但是internal_node_cell()函数返回值是4字节int指针,所以指针算数运算的单位为4个字节,需要先转换为单字节指针然后再加上偏移量

对于一个内部节点，最大的key总是它的最右边的key.对于一个叶子节点,最大的key的下标最大:

+uint32_t get_node_max_key(void* node) {
+  switch (get_node_type(node)) {
+    case NODE_INTERNAL:
+      return *internal_node_key(node, *internal_node_num_keys(node) - 1);
+    case NODE_LEAF:
+      return *leaf_node_key(node, *leaf_node_num_cells(node) - 1);
+  }
+}

Keeping Track of the Root

我们最后利用的是普通节点头部的is_root值.

记得我们使用它来决定如何分裂一个叶子节点的:

  if (is_node_root(old_node)) {
    return create_new_root(cursor->table, new_page_num);
  } else {
    printf("Need to implement updating parent after split\n");
    exit(EXIT_FAILURE);
  }
}

这里有getter & setter:

+bool is_node_root(void* node) {
+  uint8_t value = *((uint8_t*)(node + IS_ROOT_OFFSET));
+  return (bool)value;
+}
+
+void set_node_root(void* node, bool is_root) {
+  uint8_t value = is_root;
+  *((uint8_t*)(node + IS_ROOT_OFFSET)) = value;
+}

初始化每种节点都应该默认设置is_root为false:

 void initialize_leaf_node(void* node) {
   set_node_type(node, NODE_LEAF);
+  set_node_root(node, false);
   *leaf_node_num_cells(node) = 0;
 }

+void initialize_internal_node(void* node) {
+  set_node_type(node, NODE_INTERNAL);
+  set_node_root(node, false);
+  *internal_node_num_keys(node) = 0;
+}

我们应该在创建的节点为table中的第一个节点时设置is_root为true:

     // New database file. Initialize page 0 as leaf node.
     void* root_node = get_page(pager, 0);
     initialize_leaf_node(root_node);
+    set_node_root(root_node, true);
   }
 
   return table;

Printing the Tree

为了帮助我们可视化数据库的状态,我们应该更新.btree命令以打印一棵多阶树.

我将会替换现有的print_leaf_node()函数:

-void print_leaf_node(void* node) {
-  uint32_t num_cells = *leaf_node_num_cells(node);
-  printf("leaf (size %d)\n", num_cells);
-  for (uint32_t i = 0; i < num_cells; i++) {
-    uint32_t key = *leaf_node_key(node, i);
-    printf("  - %d : %d\n", i, key);
-  }
-}

用一个递归函数代替它.递归函数接受一个任意节点作为参数，然后打印该节点和所有子节点.还接受一个参数作为缩进等级,在向下递归的时候缩进等级递增.我还添加了一个小的辅助函数用于打印缩进.

+void indent(uint32_t level) {
+  for (uint32_t i = 0; i < level; i++) {
+    printf("  ");
+  }
+}
+
+void print_tree(Pager* pager, uint32_t page_num, uint32_t indentation_level) {
+  void* node = get_page(pager, page_num);
+  uint32_t num_keys, child;
+
+  switch (get_node_type(node)) {
+    case (NODE_LEAF):
+      num_keys = *leaf_node_num_cells(node);
+      indent(indentation_level);
+      printf("- leaf (size %d)\n", num_keys);
+      for (uint32_t i = 0; i < num_keys; i++) {
+        indent(indentation_level + 1);
+        printf("- %d\n", *leaf_node_key(node, i));
+      }
+      break;
+    case (NODE_INTERNAL):
+      num_keys = *internal_node_num_keys(node);
+      indent(indentation_level);
+      printf("- internal (size %d)\n", num_keys);
+      for (uint32_t i = 0; i < num_keys; i++) {
+        child = *internal_node_child(node, i);
+        print_tree(pager, child, indentation_level + 1);
+
+        indent(indentation_level + 1);
+        printf("- key %d\n", *internal_node_key(node, i));
+      }
+      child = *internal_node_right_child(node);
+      print_tree(pager, child, indentation_level + 1);
+      break;
+  }
+}

然后更新.btree调用的函数,一开始传递的缩进等级为0.

   } else if (strcmp(input_buffer->buffer, ".btree") == 0) {
     printf("Tree:\n");
-    print_leaf_node(get_page(table->pager, 0));
+    print_tree(table->pager, 0, 0);
     return META_COMMAND_SUCCESS;

这里有测试新的打印函数的代码喔!

+  it 'allows printing out the structure of a 3-leaf-node btree' do
+    script = (1..14).map do |i|
+      "insert #{i} user#{i} person#{i}@example.com"
+    end
+    script << ".btree"
+    script << "insert 15 user15 person15@example.com"
+    script << ".exit"
+    result = run_script(script)
+
+    expect(result[14...(result.length)]).to match_array([
+      "db > Tree:",
+      "- internal (size 1)",
+      "  - leaf (size 7)",
+      "    - 1",
+      "    - 2",
+      "    - 3",
+      "    - 4",
+      "    - 5",
+      "    - 6",
+      "    - 7",
+      "  - key 7",
+      "  - leaf (size 7)",
+      "    - 8",
+      "    - 9",
+      "    - 10",
+      "    - 11",
+      "    - 12",
+      "    - 13",
+      "    - 14",
+      "db > Need to implement searching an internal node",
+    ])
+  end

打印的内容被简化了,所以我们需要更新一下之前的.btree测试:

       "db > Executed.",
       "db > Executed.",
       "db > Tree:",
-      "leaf (size 3)",
-      "  - 0 : 1",
-      "  - 1 : 2",
-      "  - 2 : 3",
+      "- leaf (size 3)",
+      "  - 1",
+      "  - 2",
+      "  - 3",
       "db > "
     ])
   end

这是.btree测试的输出:

Tree:
- internal (size 1)
  - leaf (size 7)
    - 1
    - 2
    - 3
    - 4
    - 5
    - 6
    - 7
  - key 7
  - leaf (size 7)
    - 8
    - 9
    - 10
    - 11
    - 12
    - 13
    - 14

在缩进级别0，我们看到了根节点(这是个内部节点喔).size 1表示它只有一个键.在缩进级别1,有一个叶子节点,一个键和另一个叶子节点.在根节点的键(7)是它的第一个左孩子的最大的键.所有比7大的键在第二个叶子节点里.

A Major Problem

如果你观察仔细的话就会注意到我们忽略了很重要的事情.当我们尝试再插入一行时会变成这样:

db > insert 15 user15 person15@example.com
Need to implement searching an internal node

哎呀!谁写下的TODO信息? :P 😤😤

在下一章我们会继续B-tree的传奇，实现在一个多阶树中搜索.

Part 11 -Recursively Searching the B-Tree

上一章结尾我们插入第15行得到了一个错误:

db > insert 15 user15 person15@example.com
Need to implement searching an internal node

首先，用一个新的函数调用替换代码存根.

   if (get_node_type(root_node) == NODE_LEAF) {
     return leaf_node_find(table, root_page_num, key);
   } else {
-    printf("Need to implement searching an internal node\n");
-    exit(EXIT_FAILURE);
+    return internal_node_find(table, root_page_num, key);
   }
 }

该函数会用二分查找包含给定key的子节点.记住每个子节点指针的右边的key是该子节点包含的最大的key.

three-level btree

所以我们的二分查找会比较需要找到的key和子节点指针右边的key:

+Cursor* internal_node_find(Table* table, uint32_t page_num, uint32_t key) {
+  void* node = get_page(table->pager, page_num);
+  uint32_t num_keys = *internal_node_num_keys(node);
+
+  /* Binary search to find index of child to search */
+  uint32_t min_index = 0;
+  uint32_t max_index = num_keys; /* there is one more child than key */
+
+  while (min_index != max_index) {
+    uint32_t index = (min_index + max_index) / 2;
+    uint32_t key_to_right = *internal_node_key(node, index);
+    if (key_to_right >= key) {
+      max_index = index;
+    } else {
+      min_index = index + 1;
+    }
+  }

还要记住一个内部节点的子节点可能是叶子节点或者内部节点.在我们找到正确的孩子后,要调用恰当的搜索函数:

+  uint32_t child_num = *internal_node_child(node, min_index);
+  void* child = get_page(table->pager, child_num);
+  switch (get_node_type(child)) {
+    case NODE_LEAF:
+      return leaf_node_find(table, child_num, key);
+    case NODE_INTERNAL:
+      return internal_node_find(table, child_num, key);
+  }
+}

译者注: 还有一个地方需要修改-execute_insert

因为现在搜索后的cursor不一定指向根节点，所以node应该是cursor指向的节点

Tests

现在向多节点btree中插入键不再会导致错误了.然后我们可以更新下我们的测试:

       "    - 12",
       "    - 13",
       "    - 14",
-      "db > Need to implement searching an internal node",
+      "db > Executed.",
+      "db > ",
     ])
   end

我认为还可以重用一下另一个测试,就是那个试图插入1400行的.它仍然会出错，但是错误信息变了.目前该测试在程序中断的时候不能很好地处理.如果程序崩溃了，我们只需要使用目前使用的错误信息:

     raw_output = nil
     IO.popen("./db test.db", "r+") do |pipe|
       commands.each do |command|
-        pipe.puts command
+        begin
+          pipe.puts command
+        rescue Errno::EPIPE
+          break
+        end
       end

       pipe.close_write

然后这揭露了1400行测试的错误信息是这个:

     end
     script << ".exit"
     result = run_script(script)
-    expect(result[-2]).to eq('db > Error: Table full.')
+    expect(result.last(2)).to match_array([
+      "db > Executed.",
+      "db > Need to implement updating parent after split",
+    ])
   end

这看起来好像是我们to-do列表的下一个目标!

Part 12 -Scanning a Multi-Level B-Tree

目前我们的数据库程序支持构建多阶btree,但是我们在这个过程中破坏了select语句.这里有一个测试插入15行然后尝试打印它们.

+  it 'prints all rows in a multi-level tree' do
+    script = []
+    (1..15).each do |i|
+      script << "insert #{i} user#{i} person#{i}@example.com"
+    end
+    script << "select"
+    script << ".exit"
+    result = run_script(script)
+
+    expect(result[15...result.length]).to match_array([
+      "db > (1, user1, person1@example.com)",
+      "(2, user2, person2@example.com)",
+      "(3, user3, person3@example.com)",
+      "(4, user4, person4@example.com)",
+      "(5, user5, person5@example.com)",
+      "(6, user6, person6@example.com)",
+      "(7, user7, person7@example.com)",
+      "(8, user8, person8@example.com)",
+      "(9, user9, person9@example.com)",
+      "(10, user10, person10@example.com)",
+      "(11, user11, person11@example.com)",
+      "(12, user12, person12@example.com)",
+      "(13, user13, person13@example.com)",
+      "(14, user14, person14@example.com)",
+      "(15, user15, person15@example.com)",
+      "Executed.", "db > ",
+    ])
+  end

但是当我们运行这个测试的时候，实际上会发生这个:

db > select
(2, user1, person1@example.com)
Executed.

这很奇怪不是阿木.它只打印了一行数据，并且该行看起来已经损坏了(注意id和username不匹配).

产生这个问题的原因是execute_select()从table的开头开始,然后我们当前的table_start()函数返回的是根节点的下标为0的cell.但是我们的btree的根节点现在是一个内部节点，不包含任何行.所以打印出来的数据一定是从根节点还是叶子节点的时候留下来的.execute_select()真正应该返回的是最左边叶子节点的下标为0的cell.

所以让我们先清除旧的实现:

-Cursor* table_start(Table* table) {
-  Cursor* cursor = malloc(sizeof(Cursor));
-  cursor->table = table;
-  cursor->page_num = table->root_page_num;
-  cursor->cell_num = 0;
-
-  void* root_node = get_page(table->pager, table->root_page_num);
-  uint32_t num_cells = *leaf_node_num_cells(root_node);
-  cursor->end_of_table = (num_cells == 0);
-
-  return cursor;
-}

然后添加新的实现，搜索key₀(可能的最小key).即使key₀在表中不存在,该函数会返回最小的id的位置(最左边的叶子节点的开头).

+Cursor* table_start(Table* table) {
+  Cursor* cursor =  table_find(table, 0);
+
+  void* node = get_page(table->pager, cursor->page_num);
+  uint32_t num_cells = *leaf_node_num_cells(node);
+  cursor->end_of_table = (num_cells == 0);
+
+  return cursor;
+}

通过这些改动，它仍然只打印一个叶子节点的所有行:

db > select
(1, user1, person1@example.com)
(2, user2, person2@example.com)
(3, user3, person3@example.com)
(4, user4, person4@example.com)
(5, user5, person5@example.com)
(6, user6, person6@example.com)
(7, user7, person7@example.com)
Executed.
db >

因为一共有15条记录,我们的btree包含一个内部节点和两个叶子节点，就像这样:

structure of our btree

为了扫描整个表,当我们到达第一个叶子节点的末尾后需要跳到第二个叶子节点.为了实现这个操作，我们将在叶子节点的头部存储一个新的字段 - “next_leaf”,该字段的值为该叶子节点的右边的兄弟节点的page number.最右边的叶子节点的next_leaf的值为0以表示它没有右兄弟(page₀不论何时都预留给表的根节点).

更新叶子节点的头部格式以包含新的字段:

 const uint32_t LEAF_NODE_NUM_CELLS_SIZE = sizeof(uint32_t);
 const uint32_t LEAF_NODE_NUM_CELLS_OFFSET = COMMON_NODE_HEADER_SIZE;
-const uint32_t LEAF_NODE_HEADER_SIZE =
-    COMMON_NODE_HEADER_SIZE + LEAF_NODE_NUM_CELLS_SIZE;
+const uint32_t LEAF_NODE_NEXT_LEAF_SIZE = sizeof(uint32_t);
+const uint32_t LEAF_NODE_NEXT_LEAF_OFFSET =
+    LEAF_NODE_NUM_CELLS_OFFSET + LEAF_NODE_NUM_CELLS_SIZE;
+const uint32_t LEAF_NODE_HEADER_SIZE = COMMON_NODE_HEADER_SIZE +
+                                       LEAF_NODE_NUM_CELLS_SIZE +
+                                       LEAF_NODE_NEXT_LEAF_SIZE;

以及一个函数用来获取该字段:

+uint32_t* leaf_node_next_leaf(void* node) {
+  return node + LEAF_NODE_NEXT_LEAF_OFFSET;
+}

初始化一个新的叶子节点时令next_leaf为0：

@@ -322,6 +330,7 @@ void initialize_leaf_node(void* node) {
   set_node_type(node, NODE_LEAF);
   set_node_root(node, false);
   *leaf_node_num_cells(node) = 0;
+  *leaf_node_next_leaf(node) = 0;  // 0 represents no sibling
 }

当我们分裂一个叶子节点时,更新兄弟指针.旧的叶子节点的兄弟变成了新创建的叶子,然后新的叶子节点的兄弟是旧叶子节点的原兄弟,无论原兄弟是什么.

@@ -659,6 +671,8 @@ void leaf_node_split_and_insert(Cursor* cursor, uint32_t key, Row* value) {
   uint32_t new_page_num = get_unused_page_num(cursor->table->pager);
   void* new_node = get_page(cursor->table->pager, new_page_num);
   initialize_leaf_node(new_node);
+  *leaf_node_next_leaf(new_node) = *leaf_node_next_leaf(old_node);
+  *leaf_node_next_leaf(old_node) = new_page_num;

增加一个新的字段会改变一些常量:

   it 'prints constants' do
     script = [
       ".constants",
@@ -199,9 +228,9 @@ describe 'database' do
       "db > Constants:",
       "ROW_SIZE: 293",
       "COMMON_NODE_HEADER_SIZE: 6",
-      "LEAF_NODE_HEADER_SIZE: 10",
+      "LEAF_NODE_HEADER_SIZE: 14",
       "LEAF_NODE_CELL_SIZE: 297",
-      "LEAF_NODE_SPACE_FOR_CELLS: 4086",
+      "LEAF_NODE_SPACE_FOR_CELLS: 4082",
       "LEAF_NODE_MAX_CELLS: 13",
       "db > ",
     ])

现在无论何时我们想要cursor从一个叶子节点的末尾前进,我们可以检查该叶子节点是否有兄弟.如果有就跳到它那里,没有的话就意味着我们就到达了表的末尾.

@@ -428,7 +432,15 @@ void cursor_advance(Cursor* cursor) {
 
   cursor->cell_num += 1;
   if (cursor->cell_num >= (*leaf_node_num_cells(node))) {
-    cursor->end_of_table = true;
+    /* Advance to next leaf node */
+    uint32_t next_page_num = *leaf_node_next_leaf(node);
+    if (next_page_num == 0) {
+      /* This was rightmost leaf */
+      cursor->end_of_table = true;
+    } else {
+      cursor->page_num = next_page_num;
+      cursor->cell_num = 0;
+    }
   }
 }

做了这些改动之后，我们雀食打印了15行了喔…

db > select
(1, user1, person1@example.com)
(2, user2, person2@example.com)
(3, user3, person3@example.com)
(4, user4, person4@example.com)
(5, user5, person5@example.com)
(6, user6, person6@example.com)
(7, user7, person7@example.com)
(8, user8, person8@example.com)
(9, user9, person9@example.com)
(10, user10, person10@example.com)
(11, user11, person11@example.com)
(12, user12, person12@example.com)
(13, user13, person13@example.com)
(1919251317, 14, on14@example.com)
(15, user15, person15@example.com)
Executed.
db >

…但是其中的一行看起来好像损坏了.

在经过一些调试之后，我发现这个bug来自分裂叶子节点的函数:

@@ -676,7 +690,9 @@ void leaf_node_split_and_insert(Cursor* cursor, uint32_t key, Row* value) {
     void* destination = leaf_node_cell(destination_node, index_within_node);
 
     if (i == cursor->cell_num) {
-      serialize_row(value, destination);
+      serialize_row(value,
+                    leaf_node_value(destination_node, index_within_node));
+      *leaf_node_key(destination_node, index_within_node) = key;
     } else if (i > cursor->cell_num) {
       memcpy(destination, leaf_node_cell(old_node, i - 1), LEAF_NODE_CELL_SIZE);
     } else {

请记住叶子节点的每一个cell包含key和value,key在前,value在后喔:

Original leaf node format

我们把待插入的行(的value)写入了cell的开头,而这应该是存储key的地方.这意味着username的一部分变成了id(导致id大的变态).

译者注: 呃，让我来解释一下…

cell的存储格式为key+value,但是分裂函数中只写入了value,而value是key+username+email,所以即使格式错了,但是key是对的,能被正确索引.

但是读取的时候是直接读取value部分的,而这部分现在变成了username+email(本来应该是key+usn+email).

修复了bug之后,我们最终可以如期打印整个表了:

db > select
(1, user1, person1@example.com)
(2, user2, person2@example.com)
(3, user3, person3@example.com)
(4, user4, person4@example.com)
(5, user5, person5@example.com)
(6, user6, person6@example.com)
(7, user7, person7@example.com)
(8, user8, person8@example.com)
(9, user9, person9@example.com)
(10, user10, person10@example.com)
(11, user11, person11@example.com)
(12, user12, person12@example.com)
(13, user13, person13@example.com)
(14, user14, person14@example.com)
(15, user15, person15@example.com)
Executed.
db >

😼😼!一个接一个的bug,但是我们一直在前进.

直到下一次.

Part 13 - Updating Parent Node After a Split

对于史诗般的b-tree之旅的下一步,我们将要在分裂叶子节点之后处理父节点,我会使用下面的例子作为参考:

Example of updating internal node

在这个例子中,我们给树添加了key₃.这导致了左边叶子节点的分裂.在分裂之后我们通过下面这些步骤修复这棵树:

更新父节点的第一个key为最左边子节点的key_max(本例中是3).
在更新后的key后面添加一个子节点指针/key对
- 新的子节点指针指向新的子节点
- 新的key是新的子节点的key_max

那么第一件事是,用两个新函数调用替换我们的占坑代码:

update_internal_node_key() for step 1 and internal_node_insert() for step 2

@@ -670,9 +725,11 @@ void leaf_node_split_and_insert(Cursor* cursor, uint32_t key, Row* value) {
   */
 
   void* old_node = get_page(cursor->table->pager, cursor->page_num);
+  uint32_t old_max = get_node_max_key(old_node);
   uint32_t new_page_num = get_unused_page_num(cursor->table->pager);
   void* new_node = get_page(cursor->table->pager, new_page_num);
   initialize_leaf_node(new_node);
+  *node_parent(new_node) = *node_parent(old_node);
   *leaf_node_next_leaf(new_node) = *leaf_node_next_leaf(old_node);
   *leaf_node_next_leaf(old_node) = new_page_num;
 
@@ -709,8 +766,12 @@ void leaf_node_split_and_insert(Cursor* cursor, uint32_t key, Row* value) {
   if (is_node_root(old_node)) {
     return create_new_root(cursor->table, new_page_num);
   } else {
-    printf("Need to implement updating parent after split\n");
-    exit(EXIT_FAILURE);
+    uint32_t parent_page_num = *node_parent(old_node);
+    uint32_t new_max = get_node_max_key(old_node);
+    void* parent = get_page(cursor->table->pager, parent_page_num);
+
+    update_internal_node_key(parent, old_max, new_max);
+    internal_node_insert(cursor->table, parent_page_num, new_page_num);
+    return;
   }
 }

为了获取父节点的引用，我们需要在每个节点中记录指向父节点的指针.

+uint32_t* node_parent(void* node) { return node + PARENT_POINTER_OFFSET; }

@@ -660,6 +675,48 @@ void create_new_root(Table* table, uint32_t right_child_page_num) {
   uint32_t left_child_max_key = get_node_max_key(left_child);
   *internal_node_key(root, 0) = left_child_max_key;
   *internal_node_right_child(root) = right_child_page_num;
+  *node_parent(left_child) = table->root_page_num;
+  *node_parent(right_child) = table->root_page_num;
 }

现在我们需要找到在父节点中因为分裂操作而受到影响的cell.(分裂的)子节点不知道它在父节点中的cell_index,所以我们不能根据下标找到它.但是我们知道该子节点的key_max,所以我们可以在父节点中搜索这个key.

+void update_internal_node_key(void* node, uint32_t old_key, uint32_t new_key) {
+  uint32_t old_child_index = internal_node_find_child(node, old_key);
+  *internal_node_key(node, old_child_index) = new_key;
 }

函数internal_node_find_child()内部复用了一些在内部节点搜索key的代码.重构internal_node_find()以使用新的辅助函数.

-Cursor* internal_node_find(Table* table, uint32_t page_num, uint32_t key) {
-  void* node = get_page(table->pager, page_num);
+uint32_t internal_node_find_child(void* node, uint32_t key) {
+  /*
+  Return the index of the child which should contain
+  the given key.
+  */
+
   uint32_t num_keys = *internal_node_num_keys(node);
 
-  /* Binary search to find index of child to search */
+  /* Binary search */
   uint32_t min_index = 0;
   uint32_t max_index = num_keys; /* there is one more child than key */
 
@@ -386,7 +394,14 @@ Cursor* internal_node_find(Table* table, uint32_t page_num, uint32_t key) {
     }
   }
 
-  uint32_t child_num = *internal_node_child(node, min_index);
+  return min_index;
+}
+
+Cursor* internal_node_find(Table* table, uint32_t page_num, uint32_t key) {
+  void* node = get_page(table->pager, page_num);
+
+  uint32_t child_index = internal_node_find_child(node, key);
+  uint32_t child_num = *internal_node_child(node, child_index);
   void* child = get_page(table->pager, child_num);
   switch (get_node_type(child)) {
     case NODE_LEAF:

现在我们到了这一章的核心部分,实现函数internal_node_insert().我将分成几个部分来解释这玩意.

+void internal_node_insert(Table* table, uint32_t parent_page_num,
+                          uint32_t child_page_num) {
+  /*
+  Add a new child/key pair to parent that corresponds to child
+  */
+
+  void* parent = get_page(table->pager, parent_page_num);
+  void* child = get_page(table->pager, child_page_num);
+  uint32_t child_max_key = get_node_max_key(child);
+  uint32_t index = internal_node_find_child(parent, child_max_key);
+
+  uint32_t original_num_keys = *internal_node_num_keys(parent);
+  *internal_node_num_keys(parent) = original_num_keys + 1;
+
+  if (original_num_keys >= INTERNAL_NODE_MAX_CELLS) {
+    printf("Need to implement splitting internal node\n");
+    exit(EXIT_FAILURE);
+  }

根据新的子节点的key_max得到新的cell(子节点指针&键 pair)应该插入的位置的下标index.在我们看到的例子中,child_max_key是5然后下标为1.

如果内部节点没有空间来插入一个cell,抛出一个错误.我们将会在后续章实现分裂内部节点.

现在看一下函数的其余部分:

+
+  uint32_t right_child_page_num = *internal_node_right_child(parent);
+  void* right_child = get_page(table->pager, right_child_page_num);
+
+  if (child_max_key > get_node_max_key(right_child)) {
+    /* Replace right child */
+    *internal_node_child(parent, original_num_keys) = right_child_page_num;
+    *internal_node_key(parent, original_num_keys) =
+        get_node_max_key(right_child);
+    *internal_node_right_child(parent) = child_page_num;
+  } else {
+    /* Make room for the new cell */
+    for (uint32_t i = original_num_keys; i > index; i--) {
+      void* destination = internal_node_cell(parent, i);
+      void* source = internal_node_cell(parent, i - 1);
+      memcpy(destination, source, INTERNAL_NODE_CELL_SIZE);
+    }
+    *internal_node_child(parent, index) = child_page_num;
+    *internal_node_key(parent, index) = child_max_key;
+  }
+}

因为我们将最右边子节点指针与其余的子节点指针&键 pair分开来存储,所以需要特殊处理当新的子节点成为最右边子节点的情况.

在函数中,我们可能会进入else块.首先为新的cell腾出空间,将其他cell右移一个cell单位.(尽管在我们的示例中没有cell需要移动)

然后，将新的子节点指针&key pair写入index对应的cell位置.

为了减少测试用例的大小,我目前硬编码了INTERNAL_NODE_MAX_CELLS

@@ -126,6 +126,8 @@ const uint32_t INTERNAL_NODE_KEY_SIZE = sizeof(uint32_t);
 const uint32_t INTERNAL_NODE_CHILD_SIZE = sizeof(uint32_t);
 const uint32_t INTERNAL_NODE_CELL_SIZE =
     INTERNAL_NODE_CHILD_SIZE + INTERNAL_NODE_KEY_SIZE;
+/* Keep this small for testing */
+const uint32_t INTERNAL_NODE_MAX_CELLS = 3;

说到测试,我们的大量数据测试用例需要修改一下:

@@ -65,7 +65,7 @@ describe 'database' do
     result = run_script(script)
     expect(result.last(2)).to match_array([
       "db > Executed.",
-      "db > Need to implement updating parent after split",
+      "db > Need to implement splitting internal node",
     ])

Very satisfying, I know.

再加个测试来打印一棵4个节点的树.目前为止我们的测试的插入ID都是顺序的,这个测试将会以伪随机顺序插入记录.

+  it 'allows printing out the structure of a 4-leaf-node btree' do
+    script = [
+      "insert 18 user18 person18@example.com",
+      "insert 7 user7 person7@example.com",
+      "insert 10 user10 person10@example.com",
+      "insert 29 user29 person29@example.com",
+      "insert 23 user23 person23@example.com",
+      "insert 4 user4 person4@example.com",
+      "insert 14 user14 person14@example.com",
+      "insert 30 user30 person30@example.com",
+      "insert 15 user15 person15@example.com",
+      "insert 26 user26 person26@example.com",
+      "insert 22 user22 person22@example.com",
+      "insert 19 user19 person19@example.com",
+      "insert 2 user2 person2@example.com",
+      "insert 1 user1 person1@example.com",
+      "insert 21 user21 person21@example.com",
+      "insert 11 user11 person11@example.com",
+      "insert 6 user6 person6@example.com",
+      "insert 20 user20 person20@example.com",
+      "insert 5 user5 person5@example.com",
+      "insert 8 user8 person8@example.com",
+      "insert 9 user9 person9@example.com",
+      "insert 3 user3 person3@example.com",
+      "insert 12 user12 person12@example.com",
+      "insert 27 user27 person27@example.com",
+      "insert 17 user17 person17@example.com",
+      "insert 16 user16 person16@example.com",
+      "insert 13 user13 person13@example.com",
+      "insert 24 user24 person24@example.com",
+      "insert 25 user25 person25@example.com",
+      "insert 28 user28 person28@example.com",
+      ".btree",
+      ".exit",
+    ]
+    result = run_script(script)

它应该会输出这个:

- internal (size 3)
  - leaf (size 7)
    - 1
    - 2
    - 3
    - 4
    - 5
    - 6
    - 7
  - key 1
  - leaf (size 8)
    - 8
    - 9
    - 10
    - 11
    - 12
    - 13
    - 14
    - 15
  - key 15
  - leaf (size 7)
    - 16
    - 17
    - 18
    - 19
    - 20
    - 21
    - 22
  - key 22
  - leaf (size 8)
    - 23
    - 24
    - 25
    - 26
    - 27
    - 28
    - 29
    - 30
db >

仔细观察你会发现一个bug:

这里的key应该是7,而不是1!

在经过一堆debug和i后,我发现错误原因是一些错误的指针运算.

 uint32_t* internal_node_key(void* node, uint32_t key_num) {
-  return internal_node_cell(node, key_num) + INTERNAL_NODE_CHILD_SIZE;
+  return (void*)internal_node_cell(node, key_num) + INTERNAL_NODE_CHILD_SIZE;
 }

译者注: 如果你认真看的话,就应该知道我已经改正过这个错误了

INTERNAL_NODE_CHILD_SIZE的值为4.我的原意是令internal_node_cell()返回的指针地址加上4字节,但是因为internal_node_cell()返回的是一个uint32_t*指针,所以实际上加了4*sizeof(uint32_t)字节.在进行算数运算之前先把指针显式类型转换为void*类型，这样就能修复问题了.

注意!void指针的算数运算并不是C标准内容的一部分,所以可能在你的编译器上无效.未来我也许会写一篇关于可移植性的文章,但是目前我会保留void指针运算.

好了.One more step toward a fully-operational btree implementation.下一步应该是分裂内部节点.

Until then!

译者注: 原作者在2021.11.27更新了最后一章 - part 13.

然后彻底的鸽了(悲).本人本着人道主义精神,决定尽可能地狗尾续貂,至少得完成B树的完整架构.

当然,我也可能会鸽(毕竟我每天都做牛做马,如果实在没时间继续,我就鸽😤😤).

狗尾续貂

Part 14 - Splitting a Internal Node

基于目前的btree架构,我们的内部节点一共可以存储3个key,4个子节点.

在上一章的internal_node_insert()函数中,留了一个占坑if块.

然后稍作修改:

本章将主要实现分裂内部节点的操作.

Introduction

这是一棵有4个叶子节点的树:

(*指孩子,K指该子节点的最大的key)

现在叶子节点3需要进行分裂,分裂后一共有5个叶子节点，超出了内部节点的容量,所以需要分裂内部节点.

而我们新创建的函数internal_node_split_and_insert()将完成分裂操作.

在继续之前，我们先梳理一下插入操作:

根据key找到应该插入的位置-cursor(如果key重复的话,不会进行下面的步骤)
判断叶子节点是否填满 leaf_node_insert()
- 未满: 执行插入,然后结束.
- 已满: leaf_node_split_and_insert()
  - 如果该节点为根节点,那么分裂根节点并且创建一个新的根节点(内部节点) - create_new_root(),调整树的结构后结束.
  - 如果该节点非根节点,那么需要更新父节点中的key - update_internal_node_key,以及再向父节点插入一对子节点指针&key - internal_node_insert():
    - 如果父节点未满,插入cell,结束.
    - 如果父节点已满,分裂父节点: internal_node_split_and_insert()
      - 如果父节点为根节点,那么分裂根节点并且创建一个新的根节点
      - 父节点非根节点,那么需要更新父节点的父节点(即爷爷节点)的key,以及向爷爷节点插入一对子节点指针&key
        
        还需要考虑爷爷节点是否已满,所以这实际上是一个递归的过程…

而本章主要解决需要分裂的内部节点为根节点的情况.在分裂父节点之前,函数调用过程已经为我们做了一些准备工作:

待分裂的叶子节点已经分裂完毕 old & new
旧的叶子节点(old)在根节点中对应的key已经更新(update_internal_node_key).

所以类似Part 10 - Splitting Algorithm的操作,此时需要分裂的内部节点是root节点,操作有2步:

分裂root为两个内部节点(要包括待插入的cell)
创建一个新的root节点成为这两个内部节点的父节点

延续上文分裂节点3,假设节点3被分裂成了2个节点 - 3&5

那么分裂后的树应该长这样:

在part 10分裂叶子节点的时候我们将左边的节点多分配了一个cell,同样,在分裂内部节点的时候,如果不能均分,那么左边的节点多一个cell.

先在宏文件中定义分裂后的子节点指针数量:

cuint32 INTERNAL_NODE_MAX_CHILD=INTERNAL_NODE_MAX_CELLS+1;
cuint32 INTERNAL_NODE_SPLIT_RIGHT_CHILD_COUNT=(INTERNAL_NODE_MAX_CHILD+1)/2;
cuint32 INTERNAL_NODE_SPLIT_LEFT_CHILD_COUNT=INTERNAL_NODE_MAX_CHILD+1-INTERNAL_NODE_SPLIT_RIGHT_CHILD_COUNT;

注意这里的是子节点的数量,对于内部节点来说,key(或者说cell)的数量为子节点的数量-1.

Cell or Child?

在上一版本的internal_node_insert函数中,调用分裂内部节点的函数之前,就已经把key的数量加上了.

我们要把它移动到if判断之后.

因为调用internal_node_insert的时候还未将新的child ptr & key插入到内部节点中,如果先增加key的数量,会产生一些比较讨厌的问题.

例如原本right child的下标为2,num(keys)=2

现在增加了key的数量,num(keys)=3,那么在调用函数internal_node_child(node,child_num)的时候,因为子节点指针的数量为key+1,原本2 == num(keys)-1就是最右边子节点的下标,现在变成了下标为2的cell对应的子节点指针,而此时该cell还未插入内部节点中.

此外,还需要判断新增的节点与最右边子节点的位置关系.

因为internal_node_find_child(node,key)最多就到最右边的子节点,也就是说新增的节点如果插入下标为最右边节点对应的下标,不一定是该新增节点最终应该插入的位置.还要与最右边子节点的key进行比较以决定是放在最右边子节点的左边还是右边.

child_index为新增的子节点在父节点(是一个内部节点)的所有子节点指针中的顺序(从0开始),该下标不是其对应的cell的下标,因为内部节点的结构有cell(子节点指针&key)和最右子节点指针,所以用子节点下标比较方便.

Splitting Algorithm

分裂内部节点的操作和分裂叶子节点的逻辑差不多,只不过因为内部节点的特殊结构 - 元素为子节点指针&key(即cell)的数组以及一个最右子节点指针,有很多边界条件需要判断.

例如新增的节点为分裂后的节点的最右边孩子的情况.

以及原本不是最右边节点的cell,但是因为分裂操作而变成了最右边子节点指针的情况…

和分裂叶子节点一样.根据key值将内部节点分为upper和lower两个部分.upper里的任意元素的key都严格大于lower里的元素的最大的key.

我就不详细讲了,代码如下:

void internal_node_split_and_insert(Table* table,
                                    uint32_t internal_node_page_num,
                                    uint32_t child_page_num,
                                    uint32_t child_index){
    void* node=get_page(table->pager,internal_node_page_num);
    void* child=get_page(table->pager,child_page_num);
    uint32_t child_max_key=get_node_max_key(child);
    //待分裂的internal节点的原最大key,之后可能用于更新其在父节点中的key
    uint32_t old_max_key=get_internal_node_max_key(table->pager,node);

    uint32_t existing_num_child=*(internal_node_num_keys(node))+1; //已经存在的孩子的个数
    // parent origin rightest child
    uint32_t origin_rightest_child_index=existing_num_child-1;
    uint32_t origin_rightest_child_page_num=*(internal_node_right_child(node));
    void* origin_rightest_child=get_page(table->pager,origin_rightest_child_page_num);

    //right(new) node
    uint32_t new_node_page_num=get_unused_page_num(table->pager);
    void* new_node=get_page(table->pager,new_node_page_num);
    initialize_internal_node(new_node);
    *(internal_node_num_keys(new_node))=INTERNAL_NODE_SPLIT_RIGHT_CHILD_COUNT-1;

    for(int32_t i=existing_num_child;i>=0;i--){
        void* destination_node=NULL;
        uint32_t right_child_index;
        bool is_rightest=false; //是否是 目标节点 的最右边的孩子
        //在目标节点的下标.
        int index=i%INTERNAL_NODE_SPLIT_LEFT_CHILD_COUNT;

        if (i>=INTERNAL_NODE_SPLIT_LEFT_CHILD_COUNT){ // in new node
            destination_node=new_node;
            is_rightest=(index==INTERNAL_NODE_SPLIT_RIGHT_CHILD_COUNT-1);
        }else{ // in old node
            destination_node=node;
            is_rightest=(index==INTERNAL_NODE_SPLIT_LEFT_CHILD_COUNT-1);
        }

        if (i>child_index){ //在待插入元素右边的元素.
            if (is_rightest){ //如果是目标节点的最右边的子节点.
                *(internal_node_right_child(destination_node))=*(internal_node_child(node,i-1));
            }else { // 非目标节点的最右边的子节点,copy child_ptr & key
                if (i-1==origin_rightest_child_index){ //判断该节点是否为原节点的最右边的子节点
                    //赋值子节点指针
                    *(internal_node_child(destination_node,index))=origin_rightest_child_page_num;
                    //赋值key
                    *(uint32_t* )(internal_node_key(destination_node,index))=
                        get_node_max_key(origin_rightest_child);
                }
                else{ //源cell非最右边的孩子
                    memcpy(internal_node_cell(destination_node,index),
                    internal_node_cell(node,i-1),
                    INTERNAL_NODE_CELL_SIZE);
                }
            }
        }else if (i==child_index){ //待插入的元素
            if (is_rightest){
                *(internal_node_right_child(destination_node))=child_page_num;
            }else {
                //page num
                *(internal_node_child(destination_node,index))=child_page_num;
                //key
                *(internal_node_key(destination_node,index))=child_max_key;
            }
        }else{ // 在插入的元素的左边
            if (is_rightest){ //目标位置为最右边
                uint32_t page_num=*(internal_node_child(node,i));
                *(internal_node_right_child(destination_node))=page_num;
            }else{ //目标位置不是最右边
                if (i==origin_rightest_child_index){ //在原节点中为最右边的孩子.
                    *(internal_node_child(destination_node,index))=*(internal_node_child(node,i));
                    *(internal_node_key(destination_node,index))=get_node_max_key(origin_rightest_child);
                } else { //不是原节点的最右边孩子
                    memcpy(internal_node_cell(destination_node,index),
                    internal_node_cell(node,i),
                    INTERNAL_NODE_CELL_SIZE);
                }
            }
        }
    }

    // modify num of keys
    *(internal_node_num_keys(node))=INTERNAL_NODE_SPLIT_LEFT_CHILD_COUNT-1;
    *(internal_node_num_keys(new_node))=INTERNAL_NODE_SPLIT_RIGHT_CHILD_COUNT-1;
    
    //到此,internal node已经分裂为两个internal
    if (is_node_root(node)){ // 分裂的internal为root
        create_new_internal_root(table,new_node_page_num);
    } else { // 分裂的internal非root,更新parent
        //update lower key in parent
        uint32_t new_max_key=get_internal_node_max_key(table->pager,node);
        uint32_t parent_page_num=*(node_parent(node));
        void* parent=get_page(table->pager,parent_page_num);
        update_internal_node_key(parent,old_max_key,new_max_key);
        //insert new cell in parent node
        internal_node_insert(table,parent_page_num,new_node_page_num);
    }

}

注: 我也觉得写得很丑陋,但是我水平比较凑合所以将就看一下吧…

在该函数中还使用了一个新的用于获取内部节点的最大key的函数get_internal_node_max_key

uint32_t get_internal_node_max_key(Pager* pager,void* node){
    switch (get_node_type(node)){
        case NODE_INTERNAL:{
            uint32_t right_child=*(internal_node_right_child(node));
            return get_internal_node_max_key(pager,get_page(pager,right_child));
        }
        case NODE_LEAF:
            return get_node_max_key(node);
        default:
            cout<<"UNRECOGNIZED NODE TYPE: "<<get_node_type(node)<<endl;
            exit(EXIT_FAILURE);
    }
    
}

原来的获取最大key的函数get_node_max_key在处理内部节点时，不会递归搜索叶子节点,而get_internal_node_max_key()会获取该子树的最大key

Create New Root

如果分裂的内部节点为根节点,就进行分裂根节点的操作:

void create_new_internal_root(Table* table,uint32_t right_child_page_num){
    //root node(lower)
    uint32_t root_page_num=table->root_page_num;
    void* root_node=get_page(table->pager,root_page_num);

    //create a new node to be lower node
    uint32_t new_node_page_num=get_unused_page_num(table->pager);
    void* new_node=get_page(table->pager,new_node_page_num);
    initialize_internal_node(new_node);
    *(internal_node_num_keys(new_node))=*(internal_node_num_keys(root_node));
    *(node_parent(new_node))=root_page_num; // new node's parent ptr to root_page_num
    set_node_root(new_node,false);

    //copy cell from root to new node
    for(uint32_t i=0;i<*(internal_node_num_keys(root_node));i++){
        memcpy(internal_node_cell(new_node,i),
        internal_node_cell(root_node,i),
        INTERNAL_NODE_CELL_SIZE);
    }
    //rightest child of new node
    *(internal_node_right_child(new_node))=*(internal_node_right_child(root_node));

    //ROOT NODE
    set_node_root(root_node,true);
    *(internal_node_num_keys(root_node))=1;
    *(internal_node_child(root_node,0))=new_node_page_num;
    //注意,这里获取的max key是整棵子树,而不是一个internal节点的最大key
    *(internal_node_key(root_node,0))=get_internal_node_max_key(table->pager,root_node);
    *(internal_node_right_child(root_node))=right_child_page_num;

    // set Parent
    void* right_child=get_page(table->pager,right_child_page_num);
    *(node_parent(new_node))=table->root_page_num;
    *(node_parent(right_child))=table->root_page_num;

}

目前已经把原内部节点分裂成upper和lower两个部分.

根节点对应lower,right_child_page_num对应upper

首先申请一个新page,然后将根节点的数据全部拷贝进新节点new_node：

cell和最右边子节点指针,以及内部节点头部的一些信息.

因为根节点只有两个内部节点.所以只需要把new_node对应的子节点指针&key插入根节点中,然后再将根节点的right_child赋值为right_child_page_num即可.

最后给两个新的内部节点的parent指向根节点.

Test

测试我就懒得贴出来了.

在我的版本中额外加了一个.test begin num功能,用来向表中插入数据.

例如.test 10 5就是从id=10开始,连续插入5行,每行id递增.

我大概也不会完成这个项目了.

yourSql 2

Original

Part 8 - B-Tree leaf Node Format

Alternative Table Formats

Leaf Node Format

Accessing Leaf Node Fields

Changes to Pager and Table Objects

Changes to the Cursor Object

Insertion Into a Leaf Node

Command to Print Constants

Tree Visualization

Next Time

Complete Diff

Part 9 - Binary Search and Duplicate Keys

Part 10 - Splitting a Leaf Node

Splitting Algorithm

Allocating New Pages

Leaf Node Sizes

Creating a New Root

Internal Node Format

Keeping Track of the Root

Printing the Tree

A Major Problem

Part 11 -Recursively Searching the B-Tree

Tests

Part 12 -Scanning a Multi-Level B-Tree

Part 13 - Updating Parent Node After a Split

狗尾续貂

Part 14 - Splitting a Internal Node

Introduction

Cell or Child?

Splitting Algorithm

Create New Root

Test